
Sortieralgorithmen 1: Bubble Sort – leicht verständlich aber wenig effizient
Bei vielen Computerprogrammen ist es notwendig, eine Liste oder ein Array zu sortieren. Wenn darin Zahlen enthalten sind, dann findet diese Sortierung anhand der Größe statt. Bei Buchstaben oder Wörtern empfiehlt sich hingegen eine alphabetische Sortierung. Wenn Sie eine Liste von Hand sortieren, stellt das sicherlich kein großes Problem dar. Bei einem Computerprogramm ist dies jedoch nicht ganz so einfach. Hierbei ist es notwendig, sich genau zu überlegen, auf welche Weise Sie dabei vorgehen. Dafür ist ein Sortieralgorithmus notwendig – also ein festes Muster für die einzelnen Schritte, das dazu führt, dass die Liste sortiert wird. Hierfür gibt es zahlreiche unterschiedliche Lösungsansätze. In diesem Artikel soll der Bubble-Sort-Algorithmus vorgestellt werden. Hierbei handelt es sich um einen der einfachsten Sortieralgorithmen.
Grundsätzliche Überlegungen zu Sortieralgorithmen
Bevor wir mit den konkreten Details zum Bubble-Sort-Algorithmus einsteigen, sollen einige allgemeine Überlegungen zum Sortieren von Werten in einem Computerprogramm erfolgen. Dabei soll insbesondere darauf eingegangen werden, welche Aspekte bei der Bewertung eines Sortieralgorithmus von Bedeutung sind. Das ist wichtig, um die einzelnen Möglichkeiten später miteinander vergleichen zu können.
Zahlreiche unterschiedliche Lösungsansätze
Zunächst soll der Frage nachgegangen werden, weshalb es überhaupt so viele unterschiedliche Sortieralgorithmen gibt. Wenn Sie eine Liste manuell sortieren, machen Sie sich schließlich in der Regel überhaupt keine Gedanken darüber, welchen Sortieralgorithmus Sie anwenden – zumindest solange die Anzahl der Werte überschaubar ist. Hierbei reicht in der Regel ein kurzer Blick aus, um das kleinste Element in der Liste zu finden. Dieses können Sie dann an die erste Stelle der sortierten Liste setzen. Danach überprüfen Sie mit einem weiteren Blick, welches das zweitkleinste Element ist, sodass Sie dieses an die zweite Stelle setzen können. Damit fahren Sie fort, bis Sie alle Inhalte in die richtige Reihenfolge gebracht haben.
Allerdings handelt es sich hierbei um einen recht komplexen Vorgang. Das menschliche Gehirn ist hierzu in der Lage. Ein Computerprogramm hingegen nicht. Dass das Sortieren nicht ganz einfach ist, merken Sie bereits, wenn Sie eine längere Liste sortieren müssen – beispielsweise mit mehreren Hundert Einträgen. Hierbei ist ein kurzer Blick nicht mehr ausreichend, um das kleinste Element zu finden. Dabei müssen Sie die gesamte Liste durchgehen. Häufig sind auch zusätzliche Notizen erforderlich, um die Zwischenergebnisse festzuhalten. Das macht deutlich, dass es sich hierbei um einen recht komplexen Prozess handelt. Um diesen in einem Computerprogramm zu erledigen, müssen Sie ihn daher in mehrere einzelne Schritte zerlegen. Hierfür gibt es viele unterschiedliche Vorgehensweisen. Beispielsweise können Sie die Liste Schritt für Schritt durchgehen und nebeneinanderliegende Elemente vertauschen, falls sie sich nicht in der richtigen Reihenfolge befinden. Das ist zwar recht einfach, doch sind hierfür viele Durchgänge notwendig, bis die Liste sortiert ist. Andere Algorithmen unterteilen die Liste in mehrere Bestandteile und sortieren diese zunächst, bevor sie sie wieder zusammensetzen. Das ist häufig effizienter, allerdings sind solche Methoden in der Regel nicht ganz so leicht verständlich.
Die Komplexität der Algorithmen ist entscheidend
Der vorige Abschnitt hat gezeigt, dass es viele verschiedene Sortieralgorithmen gibt. Diese unterscheiden sich stark in ihrer Komplexität. Das bedeutet, dass die Zahl der hierfür erforderlichen Vergleiche und Zuweisungen enorme Unterschiede aufweisen kann. Computerprogramme dienen häufig dazu, Listen mit vielen Tausend Einträgen zu sortieren. Das macht es sehr wichtig, die Komplexität der Sortierverfahren genau zu beachten. Wenden Sie hierbei einen Algorithmus mit einer hohen Komplexität an, kann das zu erheblichen Verzögerungen bei der Ausführung führen.
Der beste Sortier-Algorithmen – abhängig vom genauen Anwendungszweck
Nun stellt sich noch die Frage, weshalb man mehrere Sortier-Algorithmen erlernen sollte. Schließlich wäre es auch möglich, einfach den besten und effizientesten Algorithmus zu verwenden. Dabei ist es jedoch wichtig, zu beachten, dass es sich nicht allgemein sagen lässt, welches der beste Sortieralgorithmus ist. Das hängt häufig vom Anwendungsfall ab. Je nach Situation und Anforderungen können unterschiedliche Algorithmen das beste Ergebnis liefern. Daher ist es nicht nur wichtig, die Funktionsweise der verschiedenen Algorithmen kennenzulernen. Darüber hinaus ist es notwendig, zu wissen, für welche Anwendungen sie sich eignen.
Der einfache Bubble-Sort-Algorithmus mit konstanten Durchläufen
Dieser Artikel befasst sich mit dem Bubble-Sort-Algorithmus. Hierbei handelt es sich um ein ausgesprochen einfaches Verfahren, um eine Liste zu sortieren. Daher ist dieser insbesondere bei Anfängern sehr beliebt. Im ersten Schritt befassen wir uns mit der Grundform dieser Vorgehensweise.
Der paarweise Vergleich der Elemente
Der Bubble-Sort-Algorithmus beruht auf einem paarweisen Vergleich nebeneinanderliegender Elemente. Dabei beginnt er mit dem Vergleich zwischen dem ersten und dem zweiten Element der Liste. Ist der zweite Wert größer als der erste, führt das Programm keine Aktion durch. Wenn jedoch das erste Element größer ist, vertauscht es die Positionen der beiden Inhalte – so wie dies in der folgenden Abbildung zu sehen ist.

Danach springt das Programm eine Position in der Liste weiter. Hier vergleicht es nun das zweite mit dem dritten Element. In unserer Beispielliste ist der dritte Wert größer als der zweite. Deshalb ist keine Veränderung notwendig. Das zeigt die folgende Abbildung. Wenn jedoch der zweite Wert größer wäre, wäre es auch hierbei notwendig, die Werte auszutauschen.
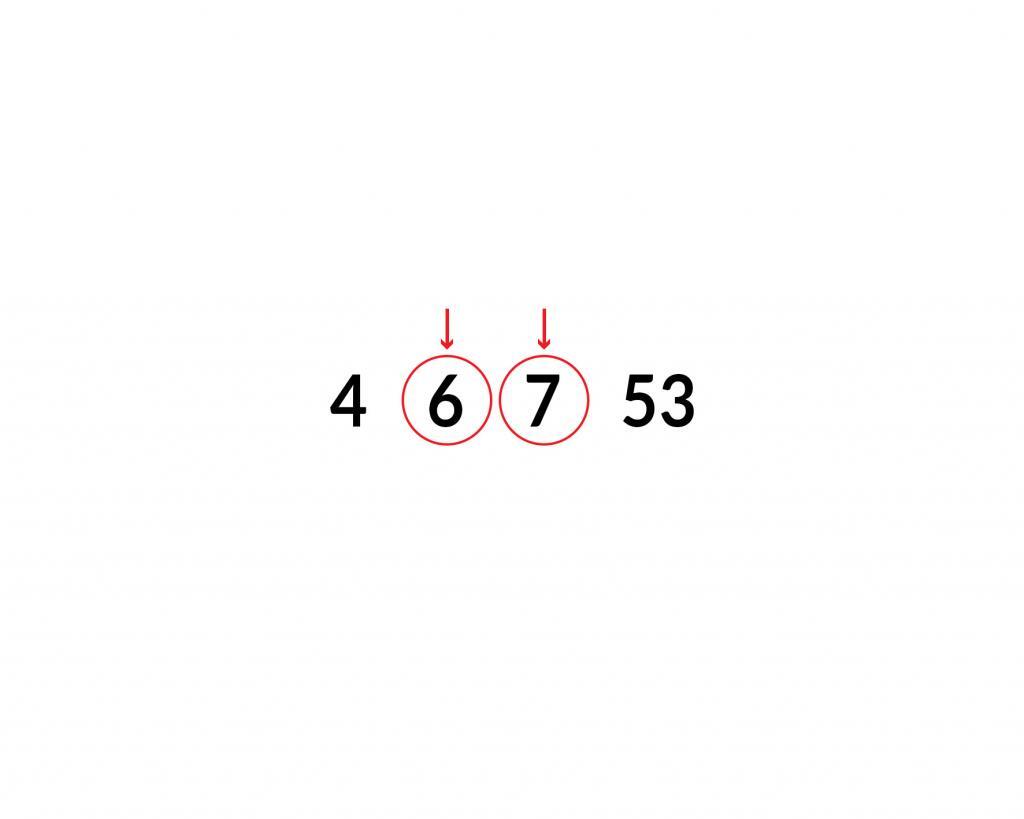
Auf diese Weise geht das Programm nun die komplette Liste durch. Die folgende Abbildung zeigt die beiden weiteren Schritte. Auch hierbei ist es erforderlich, verschiedene Werte auszutauschen. Die letzte Zeile zeigt schließlich das Ergebnis dieses Sortierverfahrens.

Weitere Durchläufe für die vollständige Sortierung der Liste
Wenn wir uns die Reihenfolge der Werte nach diesem Durchgang anschauen, sehen wir, dass die Liste noch nicht sortiert ist. Deshalb ist es notwendig, einen weiteren Durchlauf durchzuführen. Wenn wir das Verfahren aus dem vorigen Abschnitt wiederholen, erhalten wir die folgende Reihenfolge:
4 5 3 6 7
Das Ergebnis wird zwar immer besser. Dennoch ist unsere Liste noch nicht korrekt sortiert. Ein weiterer Durchlauf führt zu folgendem Ergebnis:
4 3 5 6 7
Auch hierbei ist die Liste noch nicht vollständig sortiert. Das erreichen wir erst mit dem nächsten Durchgang:
3 4 5 6 7
Nun stellt sich die Frage, wie viele Durchgänge notwendig sind. Dies hängt stets von der Länge der Liste ab. Die benötigte Anzahl ist immer um 1 geringer als die Länge der Liste. In unserem Beispiel betrug die Länge der Liste 5, sodass 4 Durchläufe erforderlich waren. Enthält die Liste beispielsweise 8 Einträge, sind 7 Durchläufe erforderlich.
Allerdings können wir uns hierbei etwas Arbeit ersparen. Der erste Durchgang stellt stets sicher, dass die größte Zahl bis ans Ende der Liste wandert. Selbst wenn sie ursprünglich ganz am Anfang steht, wird ihre Position bei jedem Vergleich gewechselt, sodass sie sich anschließend am Ende der Liste befindet. Daher ist es beim nächsten Durchgang nicht mehr notwendig, diese Position zu überprüfen, sodass wir nur noch die ersten vier Werte miteinander vergleichen müssen. Im zweiten Durchgang wandert dann die zweitgrößte Zahl an die vorletzte Stelle. Daher ist beim nächsten Durchgang noch ein Vergleich weniger notwendig. Dieses Muster setzt sich immer weiter fort, sodass wir die Zahl der Vergleiche bei jedem Durchgang weiter verkürzen können.
Ein Codebeispiel
Nun soll der Bubble-Sort-Algorithmus noch an einem kurzen Code-Beispiel vorgestellt werden. Hierfür verwenden wir die Programmiersprache C. Mit den meisten anderen gängigen Programmiersprachen würde das Programm jedoch recht ähnlich aussehen.
Für dieses Programm benötigen wir zwei ineinandergeschachtelte for-Schleifen. Die innere Schleife übernimmt den Vergleich der Werte und falls notwendig den Austausch der Positionen – also die Aufgabe, die wir im ersten Schritt beschrieben haben. Die Zahl der Durchgänge sinkt hierbei bei jedem Durchgang.
Die äußere Schleife übernimmt die Wiederholungen des entsprechenden Sortiervorgangs. Das bedeutet, dass sie lediglich die innere Schleife wiederholen muss. Wie bereits beschrieben liegt die Anzahl der Durchgänge hierbei um 1 niedriger als die Länge der Liste.
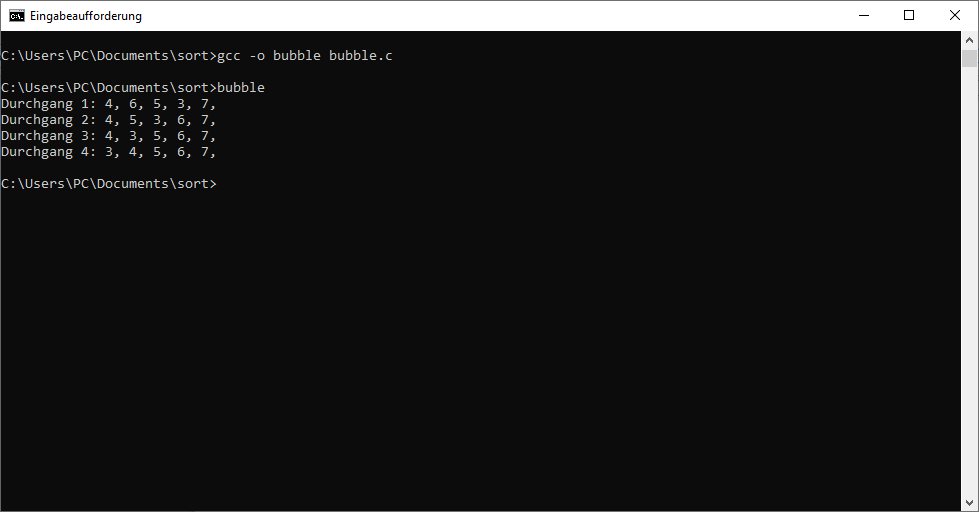
Schließlich geben wir bei jedem Durchgang die Werte des Arrays aus. Das dient jedoch nur dazu, die Veränderungen bei den einzelnen Schritten deutlich zu machen. Für den eigentlichen Sortier-Algorithmus ist dies nicht notwendig. Diese Ausgaben sind im anschließenden Screenshot zu sehen. Der Code für das Programm sieht so aus:
Eine optimierte Form des Bubble-Sort-Algorithmus
Beim eben vorgestellten Beispiel handelt es sich um die Grundfassung des Bubble-Sort-Algorithmus. Dieses lässt sich jedoch noch etwas optimieren. Das liegt daran, dass in vielen Fällen die Liste bereits nach deutlich weniger Schritten vollständig sortiert ist. In diesem Fall können wir die Schleife vorzeitig abbrechen.
Wann kann die Schleife vorzeitig abgebrochen werden?
Um herauszufinden, in welchem Fall ein vorzeitiger Abbruch möglich ist, sortieren wir nun eine weitere Liste:
4 3 7 5 6
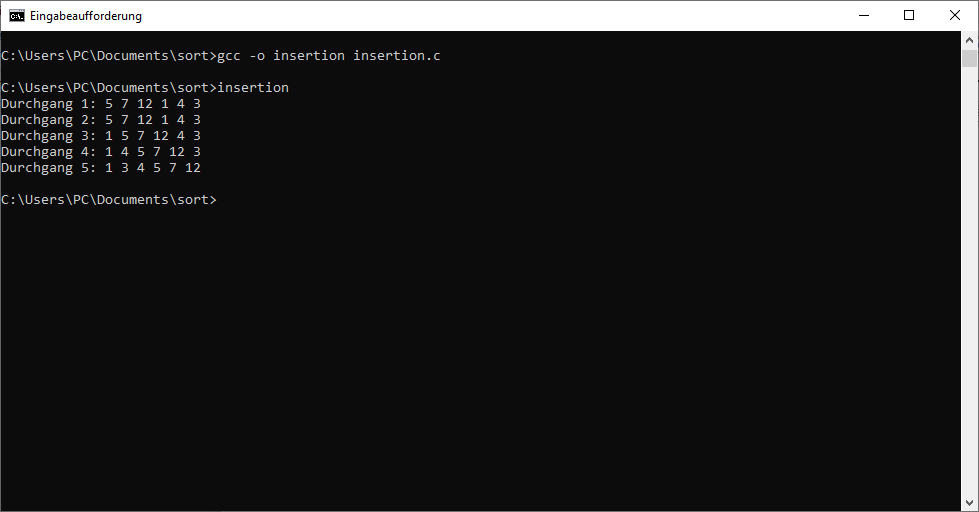
Diese hat ebenfalls fünf Elemente, sodass nach dem vorigen Beispiel eigentlich vier Durchgänge erforderlich wären. Nun überprüfen wir, was passiert, wenn wir den ersten Durchgang durchführen. Beim ersten Vergleich müssen wir den ersten und den zweiten Wert austauschen. Beim zweiten Vergleich ist keine Aktion notwendig. Beim dritten und beim vierten Vergleich sind wieder Änderungen notwendig. Die folgende Liste zeigt diese Schritte:
4 3 7 5 6
3 4 7 5 6
3 4 7 5 6
3 4 5 7 6
3 4 5 6 7
Das zeigt, dass wir mit dem ersten Durchgang die Liste bereits sortiert haben. Das bedeutet, dass wir uns alle weiteren Durchgänge eigentlich sparen könnten. Das kann den Algorithmus deutlich effizienter gestalten. Deshalb wollen wir für alle Fälle, in denen die Liste bereits vor der kompletten Anzahl der Durchläufe richtig sortiert ist, einen vorzeitigen Abbruch einfügen.
Dazu überlegen wir uns, was passiert, wenn die Liste bereits richtig sortiert ist. In diesem Fall führt das Programm keinen Austausch der Positionen aus, da die Bedingung der if-Abfrage in der inneren Schleife nie erfüllt ist. Dieses Verhalten können wir für die Steuerung der Schleife nutzen. Dafür verwenden wir eine boolesche Variable. Diese setzen wir zunächst auf true. Wenn die Reihenfolge noch nicht korrekt ist, tauschen wir nun jedoch nicht nur die Werte aus. Darüber hinaus setzen wir deren Wert auf false. Daher fügen wir in die if-Abfrage eine entsprechende Anweisung ein. Nur wenn keine Änderung der Position mehr notwendig ist, bleibt der Wert auf true. In diesem Fall können wir den Vorgang abbrechen. Daher verwenden wir diese Variable nun für die Steuerung der äußeren Schleife.
Ein Codebeispiel
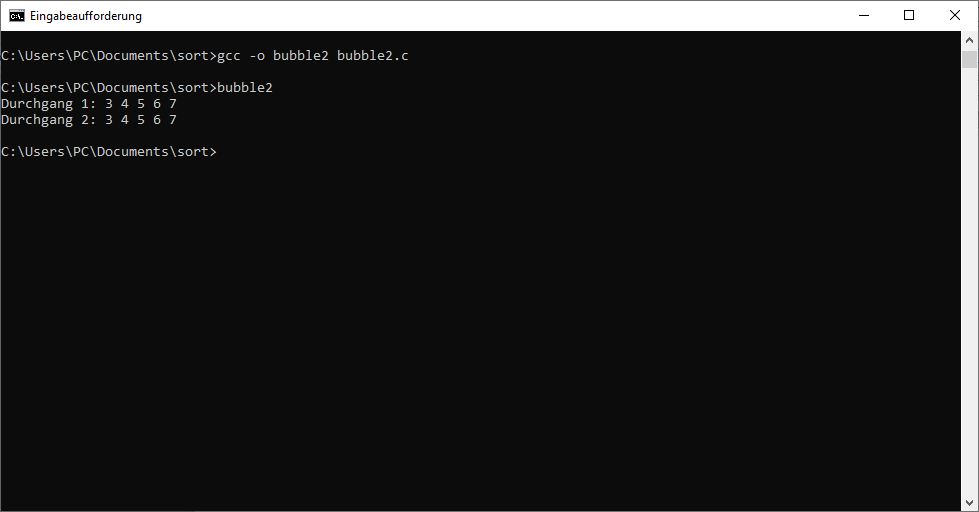
Wenn wir die angesprochenen Änderungen nun in unserem Programm umsetzen, sieht der Code dafür wie folgt aus. Der nachfolgende Screenshot zeigt, dass nun weniger Durchgänge notwendig sind, sodass wir durch diese Maßnahme die Effizienz des Programms deutlich gesteigert haben.
Die Komplexität
Nun ist es sinnvoll, einen Blick auf die Komplexität dieses Algorithmus zu werfen. Bei unserem ersten Programmbeispiel hängt die Anzahl der durchgeführten Operationen stets von der Menge der Elemente in der Liste ab. Wenn wir diese mit dem Buchstaben n bezeichnen, ergibt sich hierbei der Wert n – 1. Die Zahl der Rechenoperationen in der inneren Schleife entspricht am Anfang n. Danach nimmt sie bei jedem Durchlauf um 1 ab. Im Durchschnitt liegt sie daher bei n/2. Diese beiden Werte müssen wir nun miteinander multiplizieren. Das führt zu dem Wert ½(n² – n). Das bedeutet, dass es sich hierbei um eine quadratische Funktion handelt.
Wenn wir die optimierte Methode verwenden, entspricht die Zahl der Durchläufe hingegen nur in manchen Fällen der genannten Formel – wenn sich der kleinste Wert ursprünglich ganz am Ende der Liste befindet. Man spricht hierbei davon, dass es sich um den ungünstigsten Fall handelt. Bei anderen Listen kann die Anzahl deutlich geringer sein. Den besten Fall stellt es dar, wenn die Liste bereits komplett sortiert ist. Wenn dies zutrifft, muss das Programm sie nur ein einziges Mal durchlaufen. Es sind daher nur n Operationen erforderlich. Die Tatsächliche Anzahl der Durchläufe schwankt daher je nach Anordnung der ursprünglichen Werte zwischen n und ½(n² – n).
Vergleich mit anderen Sortieralgorithmen
Der Bubble-Sort-Algorithmus weist im ungünstigsten Fall eine hohe Komplexität auf. Das bedeutet, dass die Programme bei entsprechenden Listen sehr ineffizient arbeiten. Im besten Fall ist die Komplexität hingegen ausgesprochen gering. Darüber hinaus ist es möglich, den Durchschnittsfall zu berechnen. Das ist recht kompliziert, sodass hier nur erwähnt sei, dass das Ergebnis hierbei ebenfalls eine quadratische Funktion ist. Das zeigt, dass auch hierbei die Komplexität hoch ist.
Es gibt Algorithmen, die im ungünstigsten Fall und im Durchschnittsfall eine deutlich geringere Komplexität aufweisen als der Bubble-Sort-Algorithmus. Daher kommt dieser in der Praxis nur ausgesprochen selten zum Einsatz, da er ein sehr ineffizientes Programm zur Folge hätte. Lediglich bei Anwendungen, bei denen es wahrscheinlich ist, dass sehr günstige Fälle auftreten, kann seine Verwendung sinnvoll sein. Wenn wir beispielsweise eine bereits sortierte Liste verwenden und darin am Anfang weitere Werte einfügen, benötigt der Bubble-Sort-Algorithmus nur recht wenige Durchläufe, um die Ordnung wiederherzustellen. Daher ist seine Verwendung in solchen Fällen sinnvoll.

 C Programmieren für Einsteiger
C Programmieren für Einsteiger 






Schöner Beitrag, aber sollte im Code-Beispiel bubble_sort_1_2.c die Zeile
beendet = true;
nicht vor der for-Schleife stehen? So arbeitet das Programm fehlerhaft, wenn das Ende der Liste bereits sortiert ist.
Hallo Ralph,
Vielen Dank für Ihr positives Feedback und den Hinweis dazu!
Wir werden es überprüfen und ggf. korrigieren.
Olena vom BMU Team
Ein wunderbarer Beitrag !! — Freue mich auf den 2. Teil !!
Sehr interessant, da ich mich recht intensiv mit der C / C++ Programmierung beschäftige.
Als Rentner habe ich endlich die Zeit die ich benötige.