Mergesort: Ein effizienter Sortieralgorithmus
Eine Liste zu sortieren, stellt eine häufige Aufgabe in der Informatik dar. Hierfür gibt es viele verschiedene Vorgehensweisen – mit unterschiedlichen Vor- und Nachteilen. Deshalb stellen wir hier mehrere Sortieralgorithmen vor. Dieser Artikel befasst sich mit dem Mergesort-Algorithmus.
Die Grundidee des Mergesort-Algorithmus
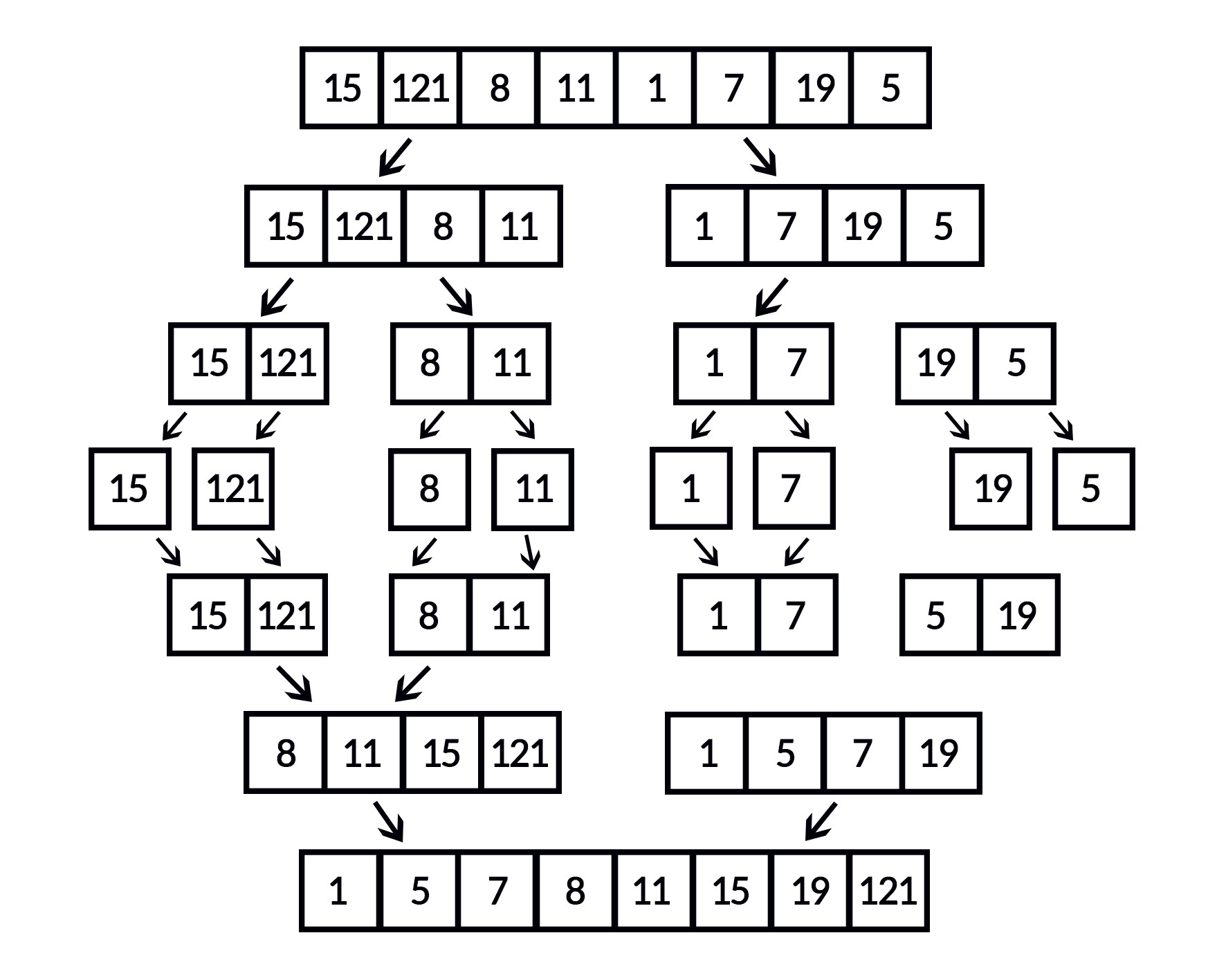
Der Mergesort-Algorithmus befolgt das Prinzip „Divide et impera!“ – häufig auch auf Deutsch als „Teile und herrsche“ oder auf Englisch als „divide and conquer“ bezeichnet. Dabei wird ein komplexes Problem – in unserem Fall das Sortieren einer Liste – so lange aufgeteilt, bis die Bearbeitung ganz einfach ist. Das sorgt für eine schnelle und effiziente Lösung der Aufgabe. Der Mergesort-Algorithmus teilt die Liste so lange auf, bis die einzelnen Teile nur noch aus einem einzelnen Element bestehen. Listen mit nur einem Element sind jedoch bereits sortiert, sodass das Problem durch die Teilung bereits gelöst ist. Danach ist es nur noch notwendig, die einzelnen Listenteile richtig zusammenzusetzen. Die folgende Abbildung verdeutlicht diese Vorgehensweise.
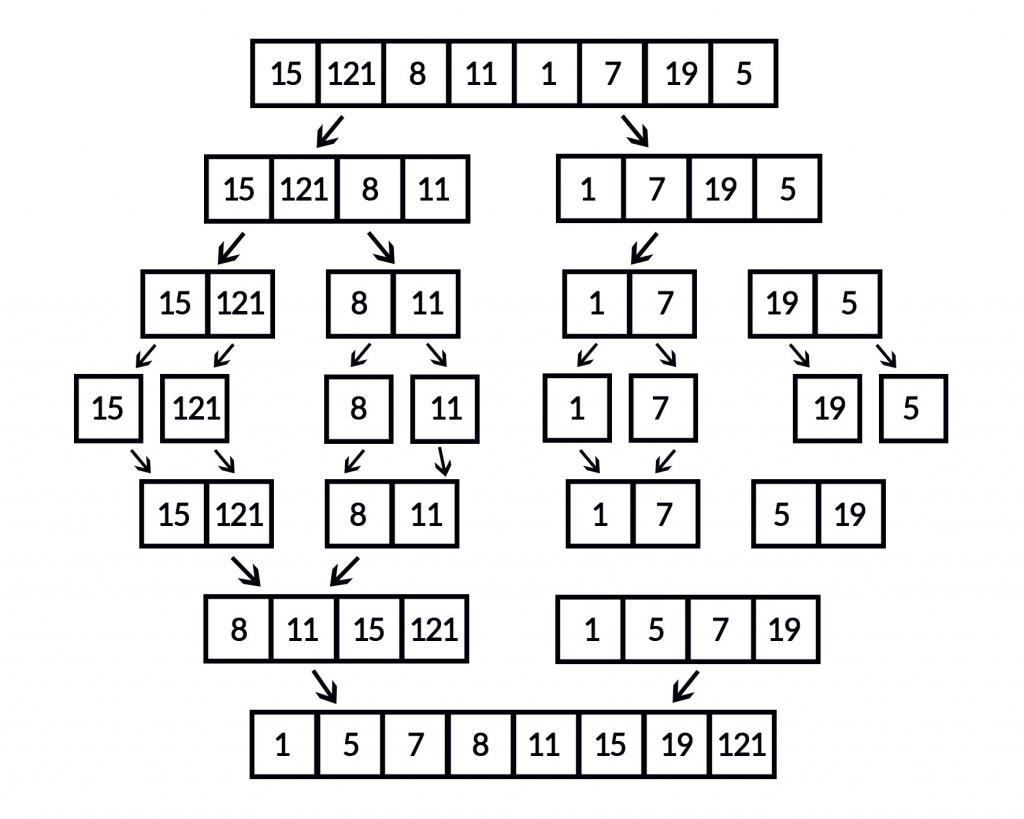
Das Aufteilen der Liste
Das Aufteilen der Liste ist beim Mergesort-Algorithmus ganz einfach. Sie müssen sie lediglich in der Mitte teilen. Das stellt einen wichtigen Unterschied zum Quicksort-Algorithmus dar – einem weiteren Sortieralgorithmus, der das Prinzip „Divide et impera!“ befolgt. Dieser sortiert die einzelnen Elemente bereits beim Aufteilen, sodass sie später ganz einfach zusammengesetzt werden können. Der Mergesort-Algorithmus teilt die Listen jedoch einfach auf, ohne dabei eine Sortierung vorzunehmen. Diese erfolgt dann beim Zusammenfügen. Die Aufteilung wird so lange fortgeführt, bis die einzelnen Teillisten jeweils nur noch ein Element aufweisen.
Das Zusammenfügen der Liste
Da die Aufteilung so lange weitergeführt wurde, bis die Teillisten nur noch aus einem einzigen Element bestehen, können Sie davon ausgehen, dass diese bereits in sich geordnet sind. Wenn Sie zwei Teillisten zusammensetzen, müssen Sie diese dabei ebenfalls ordnen. Das stellt sicher, dass auch die zusammengesetzten Teillisten geordnet sind.
Das erleichtert das Zusammensetzen in der richtigen Reihenfolge. Dabei können Sie die einzelnen Teillisten jeweils von vorne bis hinten durchgehen. Dabei vergleichen Sie stets den Eintrag an der aktuellen Position in der ersten Teilliste mit dem Eintrag an der aktuellen Position in der zweiten Teilliste. Den kleineren der beiden Werte übernehmen Sie in die Liste mit den Ergebnissen und springen in der entsprechenden Teilliste eine Position weiter. Daraufhin können Sie wieder die Werte in den beiden Teillisten an den aktuellen Positionen vergleichen. Das zeigen die folgenden Abbildungen:
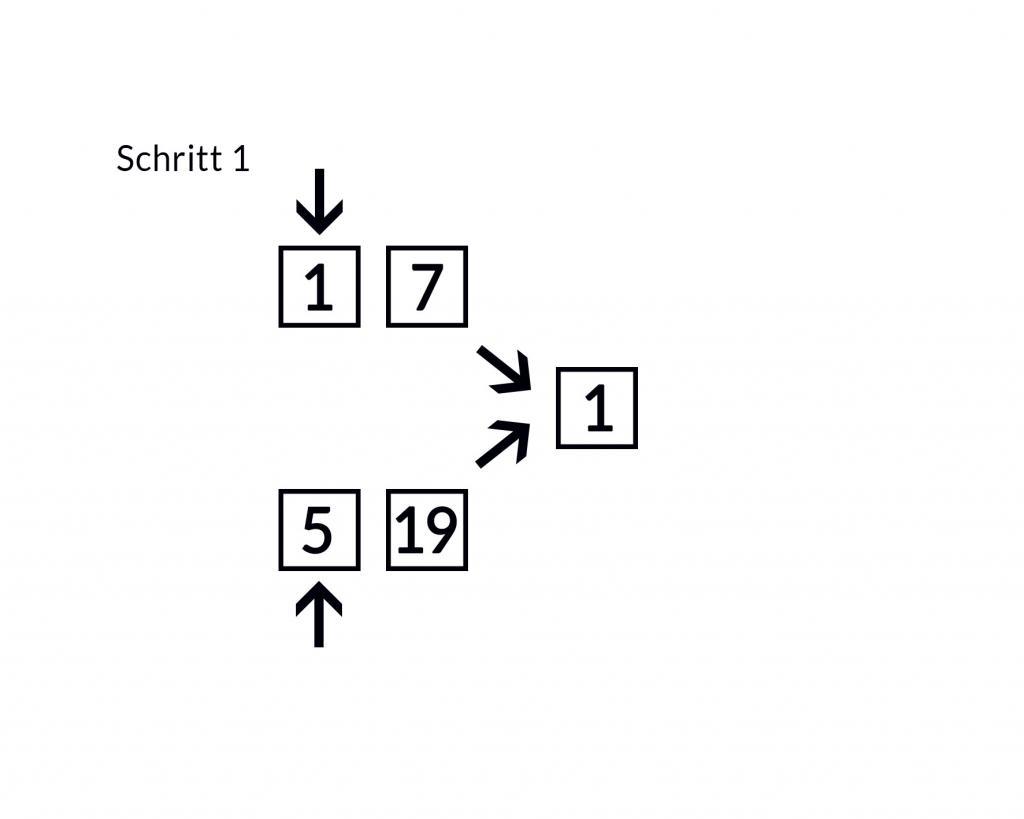
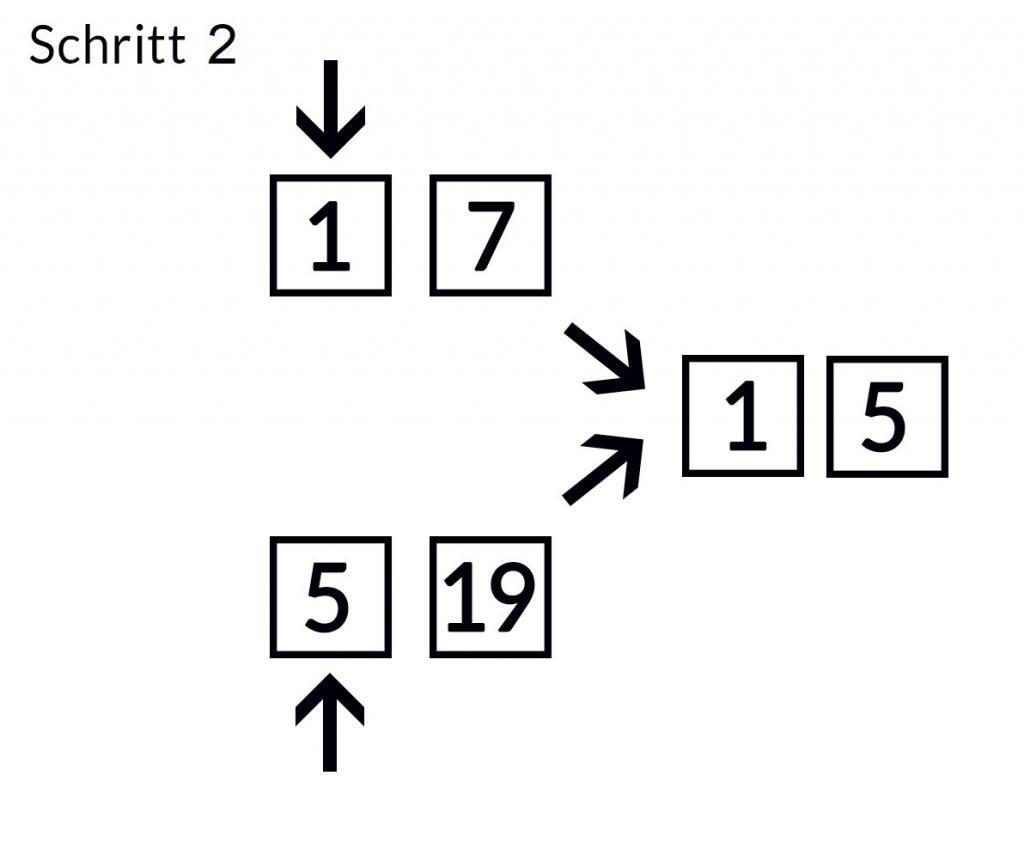
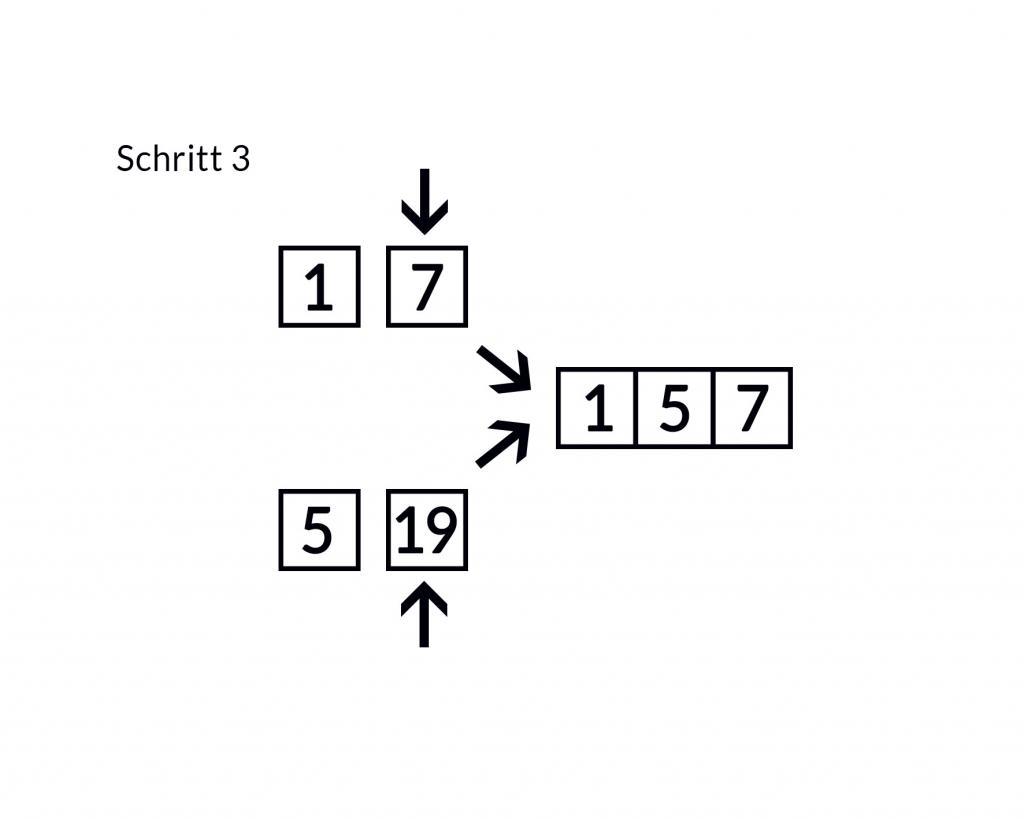
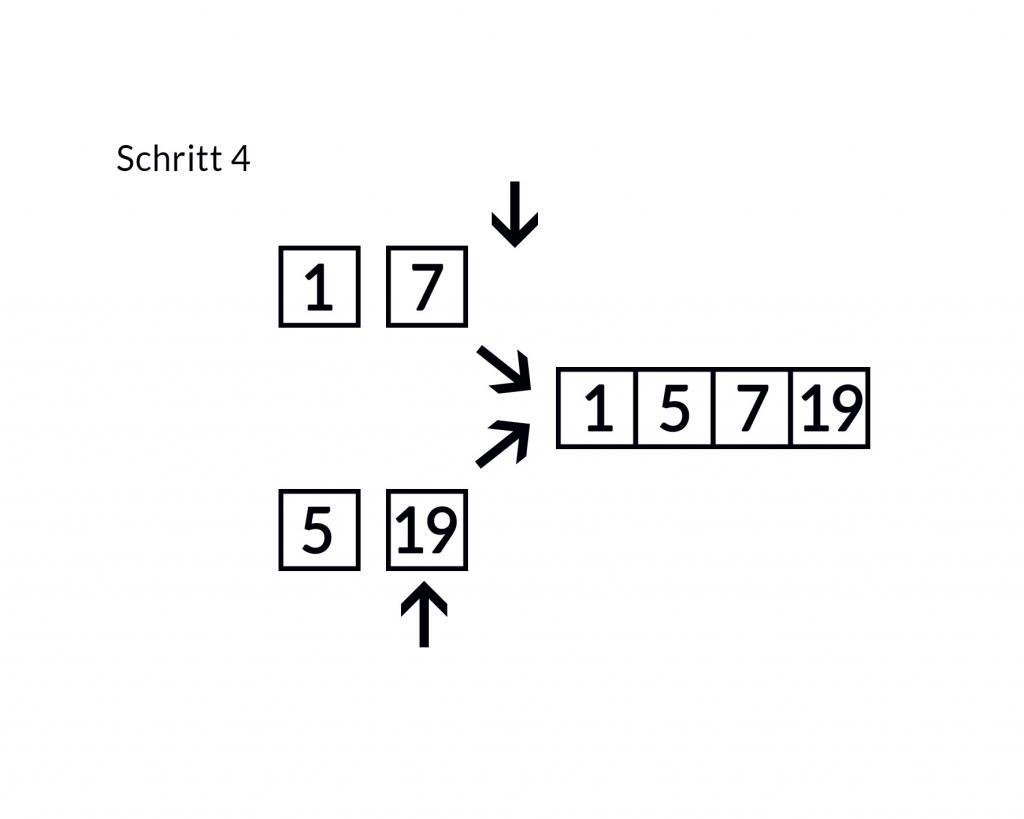
Dabei müssen Sie so lange fortfahren, bis Sie das Ende einer der beiden Teillisten erreicht haben. Danach müssen Sie lediglich die Elemente der anderen Teilliste, die nach der aktuellen Position stehen, am Ende der Liste einfügen. Da die Teillisten bereits in sich sortiert sind, wird dabei die Ordnung aufrechterhalten.
Ein Beispielprogramm für den Mergesort-Algorithmus
Nachdem die Grundlagen des Mergesort-Algorithmus vorgestellt wurden, soll nun noch ein kleines Programm entstehen, das die Funktionsweise vorstellt. Dieses erstellen wir in der Programmiersprache C.
Das Hauptprogramm
Das Hauptprogramm ist bei diesem Sortier-Algorithmus recht einfach aufgebaut. Zunächst müssen Sie hierbei ein Array erzeugen. In diesem Fall verwenden wir hierfür ganze Zahlen. Danach bestimmen wir die Größe des Arrays. In C verwenden wir hierfür die sizeof()-Funktion. Diese gibt jedoch nicht die Zahl der Felder, sondern die Größe des Arrays in Bytes zurück. Um die Zahl der Felder zu ermitteln, müssen wir diesen Wert dann noch durch die Größe eines einzelnen Arrayfelds teilen. Anschließend erzeugen wir ein weiteres Array mit genau der gleichen Größe. Dieses benötigen wir später, um die Inhalte zwischenzuspeichern. Bislang müssen wir es jedoch noch nicht mit Werten füllen:
Zunächst soll das Programm das ursprüngliche Array ausgeben. Dazu verwenden wir eine Hilfsfunktion mit der Bezeichnung arrayAusgeben(), die wir im Anschluss erstellen werden. Danach rufen wir die Funktion mergeSort() auf. Dieser übergeben wir das unsortierte Array sowie das zweite Array für die Zwischenspeicherung. Außerdem müssen wir die Anfangs- und die Endposition des Bereichs angeben, den wir sortieren wollen. Da wir beim ersten Aufruf das gesamte Array sortieren möchten, geben wir als Anfangspunkt den Wert 0 vor. Als Endpunkt verwenden wir die Position des letzten Elements. Diese ist um 1 niedriger als die Größe des Arrays:
Abschließend geben wir noch das sortierte Array aus. Auch hierfür verwenden wir wieder die Hilfsfunktion arrayAusgeben(). Damit ist das Hauptprogramm bereits abgeschlossen:
Hilfsfunktion für die Ausgabe des Arrays
Die Hilfsfunktion für die Ausgabe des Arrays ist ganz einfach aufgebaut: Sie geht dieses lediglich in einer for-Schleife durch und gibt die einzelnen Werte aus. Daher sind hierfür keine weiteren Erklärungen notwendig:
Die rekursive mergeSort()-Funktion
Nun müssen wir die mergeSort()-Funktion erstellen. Dieser haben wir das ursprüngliche Array und das Hilfs-Array übergeben. Außerdem haben wir den Anfangs- und den Endpunkt des Bereichs erhalten, den wir sortieren möchten.
Die Aufgabe dieser Funktion besteht darin, den zu sortierenden Bereich in zwei Teilbereiche zu unterteilen und diese dann einzeln zu sortieren. Das ist jedoch nur dann möglich, wenn der entsprechende Bereich mehr als ein Element enthält. Wenn nur noch ein Element enthalten ist, ist keine weitere Sortierung notwendig. Daher müssen wir in diesem Fall keine Aktion durchführen. Bei Bereichen mit nur einem Element sind der linke und der rechte Rand identisch. Sind hingegen mehrere Elemente enthalten, ist der rechte Rand größer als der linke Rand. Daher stellen wir den kompletten Inhalt der Funktion in die folgende if-Abfrage:
if (linkerRand < rechterRand)
Nun müssen wir die Mitte bestimmen. Dazu addieren wir den rechten und den linken Rand und Teilen das Ergebnis durch 2:
int mitte = (linkerRand + rechterRand) / 2;
Der nächste Schritt besteht darin, die einzelnen Teilbereiche zu sortieren. Das erledigen wir, indem wir für jeden von ihnen erneut die mergeSort()-Funktion aufrufen:
mergeSort(arr, arr2, linkerRand, mitte); mergeSort(arr, arr2, mitte + 1, rechterRand);
Zum Abschluss müssen wir die beiden Teilbereiche wieder zusammensetzen. Dazu verwenden wir die Funktion merge(), die wir im Anschluss erstellen werden. Diese benötigt die beiden Arrays sowie den rechten und den linken Rand und den Mittelwert:
merge(arr, arr2, linkerRand, mitte, rechterRand);
Damit ist auch diese Funktion abgeschlossen:
Die Funktion merge() zum Zusammenfügen des Arrays
Die anspruchsvollste Aufgabe bei der Implementierung des Mergesort-Algorithmus besteht darin, die einzelnen Teilbereiche richtig zusammenzufügen. Dazu benötigen wir mehrere Schleifen mit insgesamt drei Zählern, die wir zu Beginn erstellen. Außerdem müssen wir die Größe der beiden Teilbereiche – vom linken Rand bis einschließlich der Mittelposition und ab der Mitte bis zum rechten Rand – ermitteln:
Der nächste Schritt besteht dann darin, die Werte der beiden Teilbereiche nacheinander in das Hilfs-Array zu kopieren. Dazu verwenden wir zwei einfache for-Schleifen:
Nun beginnt der eigentliche Sortiervorgang. Dabei verwenden wir den Zähler i für den Bereich im Hilfsarray, in dem wir den ersten Teilbereich gespeichert haben und den Zähler j für den zweiten Teilbereich. Außerdem ist der Zähler k notwendig, um die sortierten Werte direkt im ursprünglichen Array festzuhalten. Wie bereits beschrieben, gehen wir dabei die einzelnen Teilbereiche Position für Position durch und übernehmen den kleineren der beiden Werte und tragen ihn in das ursprüngliche Array ein. Den Zähler für den Teilbereich, der den kleineren Wert enthalten hat, müssen wir dann um 1 erhöhen. Danach erhöhen wir auch den Zähler k, damit der nächste Wert in der darauffolgenden Position im ursprünglichen Array festgehalten wird:
Wenn wir das Ende eines der beiden Bereiche erreicht haben, wird die Schleife beendet. Im anderen Teilbereich bleiben jedoch noch einige Werte zurück. Diese müssen wir dann noch in das ursprüngliche Array eintragen. Da wir nicht wissen, in welchem der beiden Teile die Werte übrig geblieben sind, benötigen wir hierfür zwei Schleifen:
Damit haben wir die einzelnen Teilbereiche richtig zusammengefügt und damit die Funktion merge() abgeschlossen. Ihr kompletter Code sieht wie folgt aus:
Damit lässt sich das Programm bereits ausführen. Das Ergebnis ist in der folgenden Abbildung zu sehen:
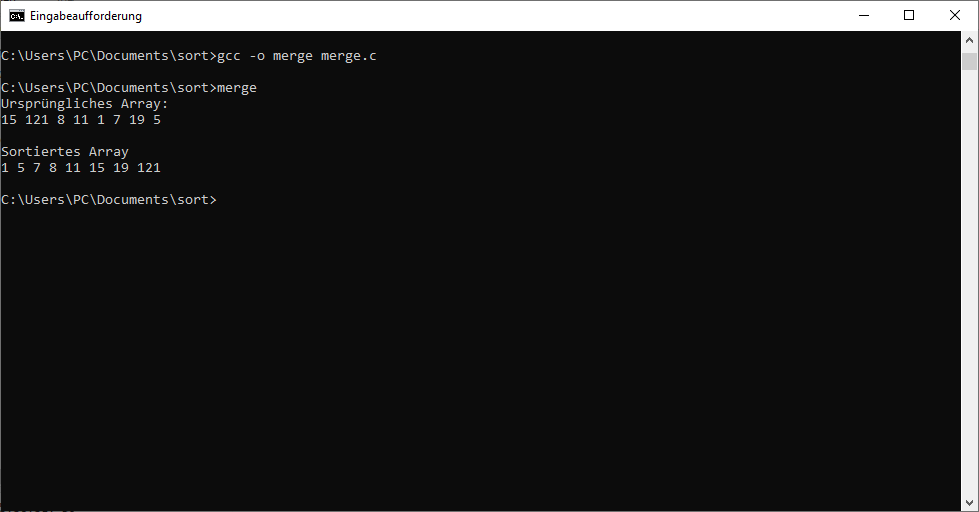
Mergesort im Vergleich zu anderen Sortieralgorithmen
Hinsichtlich der Anzahl der benötigten Rechenschritte ist der Mergesort-Algorithmus sehr effizient. Er weist hierbei sowohl bei einer durchschnittlichen Verteilung als auch im schlechtesten Fall eine logarithmische Funktion auf. Damit ist er sogar noch effizienter als der Quicksort-Algorithmus, der im schlechtesten Fall eine quadratische Funktion aufweist. Auch im Vergleich zu einfacheren Algorithmen wie Bubblesort oder Insertionsort ist die Effizienz deutlich höher. Der Nachteil besteht darin, dass Sie hierbei einen zusätzlichen Zwischenspeicher benötigen, der genauso groß wie die eigentliche Liste sein muss. Daher ist die Effizienz hinsichtlich des Speicherplatzes deutlich geringer als bei allen übrigen genannten Algorithmen.