Sortieralgorithmen 2: Quicksort – der effiziente Algorithmus
Eine Liste oder ein Array zu sortieren – entweder nummerisch oder alphabetisch – stellt in der Informatik eine sehr häufige Aufgabe dar. Was auf den ersten Blick recht einfach erscheint, ist jedoch keine ganz triviale Tätigkeit. Hierfür gibt es verschiedene Algorithmen, die auf ganz unterschiedliche Weise ans Ziel kommen. Weshalb es mehrere Sortieralgorithmen gibt und welche Unterschiede dabei zu berücksichtigen sind, haben wir bereits im ersten Teil dieser Reihe beschrieben, der sich mit dem Bubble-Sort-Algorithmus befasst hat. Der zweite Teil widmet sich nun dem Quicksort-Algorithmus. Dieser zeichnet sich durch eine hohe Effizienz aus und bietet sich daher in erster Linie für das Sortieren umfangreicher Listen an.
Die Grundidee des Quicksort-Algorithmus
Der Quicksort-Algorithmus befolgt das Prinzip „Teile und herrsche“ – beziehungsweise nach dem lateinischen Original „Divide et impera!“. Dieses stellt einen wichtigen Ansatz dar, um ein Problem in der Informatik zu lösen. Das Ziel besteht hierbei darin, ein komplexes Grundproblem in einzelne Teile zu zerlegen – so lange, bis dieses einfach zu lösen ist. Um die Funktionsweise dieses Algorithmus an einem Beispiel zu verdeutlichen, verwenden wir die Liste, die in der folgenden Abbildung zu sehen ist.

Diesem Prinzip folgend, zerteilt der Quicksort-Algorithmus die Liste zunächst in zwei Teile. Dabei stellt er sicher, dass die Werte im ersten Teil der Liste alle kleiner oder gleich groß wie die Werte im zweiten Teil der Liste sind. Das wird erreicht, indem ein Trenner festgelegt wird. Dabei kann es sich um ein beliebiges Element einer unsortierten Liste handeln. Es ist üblich, das letzte Element zu diesem Zweck zu verwenden. Es wäre aber auch möglich, das erste Element, das mittlere Element oder ein vollkommen zufälliges Element hierfür zu nutzen. Die Liste wird dann anhand dieses Trenners aufgeteilt. Alle Elemente, die kleiner als dieser sind, müssen vor ihm stehen. Alle Elemente, die größer sind, stehen hingegen nach ihm. Sollten auch Werte in der Liste enthalten sein, die die gleiche Größe wie der Trenner aufweisen, können wir frei entscheiden, ob wir diese in den ersten oder in den zweiten Teil der Liste einfügen. Diese Aufteilung stellt eine vergleichsweise einfache Aufgabe dar, die mit wenigen Schritten zu lösen ist. Das Ergebnis ist in der nächsten Abbildung zu sehen. Dabei haben wir das letzte Element als Trenner ausgewählt und die Liste entsprechend angepasst. Er ist in der Abbildung in roter Farbe markiert.

Es ist zu sehen, dass die beiden Teile der Liste für sich genommen nicht sortiert sind. Allerdings haben wir auf diese Weise erreicht, dass alle Zahlen, die größer als der Trenner sind, hinter diesem stehen und alle kleineren Zahlen vor ihm. Wenn wir nun diese beiden Teilbereiche sortieren, ist sichergestellt, dass die gesamte Liste sortiert ist. Daher stellt dies die nächste Aufgabe dar. Auch hierfür wenden wir wieder den Quicksort-Algorithmus an. Wir beginnen mit dem ersten Teil, also mit allen Werten, die kleiner als der Trenner sind. Den zweiten Teil lassen wir vorerst unverändert. In unserem Beispiel umfasst dieser die Positionen 1 bis 3. Den Trenner selbst müssen wir nicht mehr berücksichtigen, da sich dieser bereits an der richtigen Stelle befindet. Nun wenden wir den Quicksort-Algorithmus auf diesen Bereich an. Wir verwenden wieder die letzte Zahl des entsprechenden Teilbereichs als Trenner. Das Ergebnis ist in der folgenden Abbildung zu sehen.
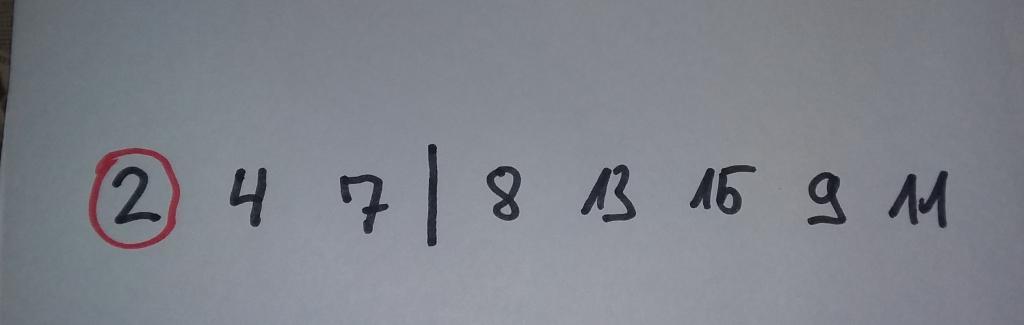
Nach diesem Prozess steht der Trenner der Teilliste ganz am Anfang. Wenn wir nun die Liste nach dem gleichen Muster weiter unterteilen, stellen wir fest, dass der vordere Bereich kein Element mehr aufweist. Daher ist es nicht mehr notwendig, diesen zu sortieren. Das Gleiche wäre der Fall, wenn er nur ein einziges Element enthalten würde. Daher brechen wir den Vorgang in diesen beiden Fällen ab. Anschließend können wir uns dem zweiten Teil der vorderen Teilliste widmen. Dieser enthält noch zwei Elemente, sodass ein weiterer Durchgang erforderlich ist. Da sich die beiden Werte jedoch bereits durch Zufall in der richtigen Reihenfolge befinden, ist keine Umstellung notwendig. Wenn wir daraufhin auf diese beiden Teilbereiche den Quicksort-Algorithmus erneut anwenden, haben die entsprechenden Bereiche wieder die Länge 0 oder 1, sodass wir den Vorgang abbrechen können. Auf diese Weise haben wir bereits erreicht, dass der komplette Bereich, der nach der ersten Teilung vor dem Trenner stand, richtig sortiert ist. Deshalb können wir uns nun der zweiten Hälfte der Liste zuwenden. Auch hier wenden wir wieder den Quicksort-Algorithmus an. Das Ergebnis zeigt die folgende Abbildung.
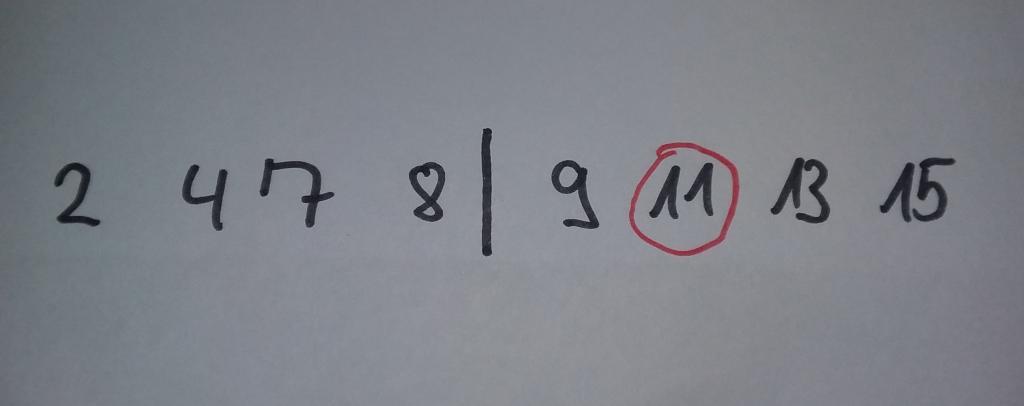
Der Bereich vor dem Trenner weist nun wieder die Größe 1 auf, sodass dieser Teil beendet wird. Beim zweiten Abschnitt kommt es zu einem weiteren Durchgang. Da sich die Zahlen hierbei jedoch wieder durch Zufall in der richtigen Reihenfolge befinden, wird die Reihenfolge nicht geändert. Wenn wir das vorige Bild nochmals genau betrachten, stellen wir fest, dass wir dabei die gesamte Liste bereits komplett sortiert haben.
Die rekursive Quicksort-Funktion
Nun wollen wir ein kleines Beispielprogramm für den Quicksort-Algorithmus erstellen. Dafür verwenden wir die Programmiersprache C. Doch würde das entsprechende Beispiel in den meisten weiteren gängigen Programmiersprachen recht ähnlich aussehen, sodass es sich leicht übertragen lässt.
Die Ausführungen im vorigen Abschnitt haben gezeigt, dass der Quicksort-Algorithmus die Liste unterteilt und danach auf die einzelnen Teile wieder den Quicksort-Algorithmus anwendet. Das erreichen wir, indem wir eine Funktion – beziehungsweise eine Methode bei objektorientierten Programmiersprachen – erstellen, die sich selbst aufruft. Das wird als rekursive Funktion bezeichnet.
Zunächst muss jedoch eine Abbruchbedingung vorgegeben werden. Diese zeigt an, wann der Sortieralgorithmus sein Ziel erreicht hat. Wir haben gesagt, dass dies der Fall ist, wenn der zu sortierende Bereich nur ein oder gar kein Element enthält. In unserer Funktion arbeiten wir dabei jeweils mit der linken und der rechten Grenze der einzelnen Bereiche. Das bedeutet, dass eine weitere Sortierung nur dann notwendig ist, wenn der Abstand zwischen dem linken und dem rechten Rand mindestens 2 beträgt. Daher fügen wir die folgende Bedingung ein: (links < rechts – 1).
Wenn diese Bedingung nicht erfüllt ist, ist der entsprechende Bereich bereits sortiert, sodass keine weitere Aktion mehr notwendig ist. Wenn eine weitere Sortierung erforderlich ist, teilen wir die Liste in zwei Bereiche und ordnen die Elemente so an, dass alle kleineren Werte vor dem Teiler und alle größeren Werte nach ihm stehen. Hierfür rufen wir lediglich die Funktion teilen() auf, die wir später erstellen werden. Diese ordnet die Liste nicht nur nach unseren Vorgaben. Darüber hinaus gibt sie die Position des Trenners zurück.
Diese Position nutzen wir nun, um die Liste weiter zu sortieren. Dazu rufen wir nun wie bereits beschrieben unsere Quicksort-Funktion erneut auf – einmal für den Bereich vor dem Trenner und einmal für den Bereich nach dem Trenner.
Der Code für die entsprechende Funktion sieht wie folgt aus;
Die Funktion zum Teilen und Ordnen der Liste
Nun müssen wir die Funktion zum Teilen der Liste erstellen, die wir in der quickSort()-Funktion aufgerufen haben. Diese erhält als Übergabewerte neben der Liste auch den linken und den rechten Rand des zu überprüfenden Bereichs.
Zunächst legt sie als Trenner den letzten Wert des entsprechenden Listenbereichs fest. Danach erstellt sie den Zähler i und gibt ihm die Position, die um 1 niedriger als der linke Rand liegt. Er liegt daher zunächst außerhalb des Bereichs, den wir überprüfen. Danach erstellen wir eine Schleife mit einem weiteren Zähler: j. Dieser geht die Liste Schritt für Schritt durch und überprüft, ob die Werte kleiner als der Trenner sind. Trifft dies nicht zu, nehmen wir keine Aktion vor. Finden wir hingegen einen Wert, der kleiner als der Trenner ist, passen wir die Liste entsprechend an. Dazu erhöhen wir zunächst die Position des Zählers i um 1. Danach vertauschen wir den Wert, der an dieser Stelle steht, mit dem Wert, den wir gerade mit dem Zähler j aufgespürt haben. Diese Vorgehensweise stellt sicher, dass alle Werte, die vor dem Zähler i stehen, kleiner als der Trenner sind. Alle Werte, die hingegen zwischen i und j stehen, sind größer oder gleich groß wie der Trenner. Wenn wir damit so lange fortfahren, bis der Zähler j das vorletzte Feld der Liste – also die Position vor unserem Trenner – erreicht hat, ist sichergestellt, dass der komplette Bereich vor i kleiner als der Trenner ist und der komplette Bereich danach mindestens so groß wie der Trenner ist.
Nun müssen wir nur noch den Trenner an die richtige Stelle setzen. Dazu tauschen wir diesen einfach mit dem Wert nach i aus. Damit haben wir der Liste die gewünschte Struktur gegeben. Abschließend geben wir noch die Position des Trenners zurück.
Wenn wir diese Vorgaben in der Funktion teilen() umsetzen, sieht diese wie folgt aus:
Das Hauptprogramm
Nun müssen wir nur noch das Hauptprogramm erstellen. Dieses erzeugt lediglich ein Array, das unsortierte Werte enthält. Da es in C etwas komplizierter ist, die Länge eines Arrays zu bestimmen, halten wir diesen Wert in der Variable n fest. Danach rufen wir die Funktion quickSort() auf und geben anschließend die sortierte Liste aus. Das Ergebnis ist im nachfolgenden Screenshot zu sehen:

Quicksort: ein häufig verwendeter Sortieralgorithmus
Wenn Sie bereits unseren Artikel zum Bubble-Sort-Algorithmus gelesen haben, stellen Sie sicher fest, dass ein Programm für das Quicksort-Verfahren deutlich aufwendiger ist. Daher ist dieser Algorithmus insbesondere bei Anfängern nicht allzu beliebt. Allerdings bietet er einen großen Vorteil: Er weist eine deutlich geringere Komplexität an. Dieser Wert gibt die Größenordnung der Anzahl der Rechenschritte an, die für die Sortierung einer Liste notwendig sind. Diese folgt beim Quicksort-Algorithmus im durchschnittlichen Fall einer logarithmischen Gleichung. Beim Bubble-Sort-Algorithmus handelt es sich hingegen hierbei um eine quadratische Gleichung. Das macht insbesondere bei großen Listen einen deutlichen Unterschied. Aus diesem Grund kommt der Quicksort-Algorithmus in der Praxis sehr häufig zum Einsatz, sodass es für jeden Informatiker sehr wichtig ist, ihn genau zu verstehen.