Sortieralgorithmen 3: Insertion Sort – leicht verständliches Sortierverfahren
Viele Computerprogramme dienen dazu, umfangreiche Daten zu verwalten. Um hierbei sinnvolle Strukturen zu schaffen, ist es wichtig, die Daten zu sortieren. Was auf den ersten Blick wie eine einfache Aufgabe aussieht, entpuppt sich für unerfahrene Programmierer jedoch häufig als ein großes Problem. Um Ordnung in einen Datensatz zu bringen, kommen mehrere Vorgehensweisen zum Einsatz. Manche von ihnen sind in ihrer Funktionsweise recht einfach verständlich, sie machen jedoch bei größeren Listen unzählige Rechenschritte notwendig, sodass sie sehr ineffizient arbeiten. Andere Alternativen sind zwar in ihrem Aufbau schwerer zu verstehen, doch benötigen sie deutlich weniger Rechenkapazität und sind daher vorzuziehen. Im ersten Teil unserer Reihe zu den Sortieralgorithmen haben wir uns bereits mit der Frage beschäftigt, weshalb es hierfür verschiedene Vorgehensweisen gibt und auf welche Unterschiede dabei zu achten ist. Wenn Sie sich zu diesem Thema informieren wollen, können Sie diese Inhalte im Artikel zum Bubble-Sort-Algorithmus nachlesen. An dieser Stelle fahren wir daher ohne weitere Einführung mit der Erklärung des Insertion-Sort-Algorithmus fort.
Insertion Sort: die Grundidee
Der Insertion-Sort-Algorithmus gehört zu den Sortieralgorithmen, deren Ablauf recht einfach zu verstehen ist. Er besteht darin, den entsprechenden Datensatz von Anfang bis Ende durchzugehen. Dabei wird das aktuelle Element jeweils entnommen und anschließend an der passenden Stelle eingeordnet. Dabei wäre es möglich, die entnommenen Werte in eine neue Liste einzuordnen. Das wäre jedoch wenig effizient. Stattdessen ordnen wir sie am Anfang der bestehenden Liste an. Diese Funktionsweise wird nun im folgenden Abschnitt an einem konkreten Beispiel erklärt.
Demonstration an einem einfachen Beispiel
Damit die Erklärung des Insertion-Sort-Algorithmus anschaulich und leicht zu verstehen wird, erklären wir diese an einer kleinen Beispielliste. Diese enthält die folgenden Zahlen: 7, 5, 12, 1, 4, 3.
Wenn wir den Insertion-Sort-Algorithmus anwenden, beginnen wir stets mit dem zweiten Element. Dieses vergleichen wir mit dem Element, das an erster Stelle steht. Ist das zweite Element größer als das erste Element, führen wir keine Aktion durch. Ist es hingegen kleiner, vertauschen wir die Inhalte der beiden Listenfelder. In unserer Beispielliste ist das zweite Element kleiner als das erste. Wie in der folgenden Abbildung zu sehen ist, müssen wir diese daher miteinander vertauschen.
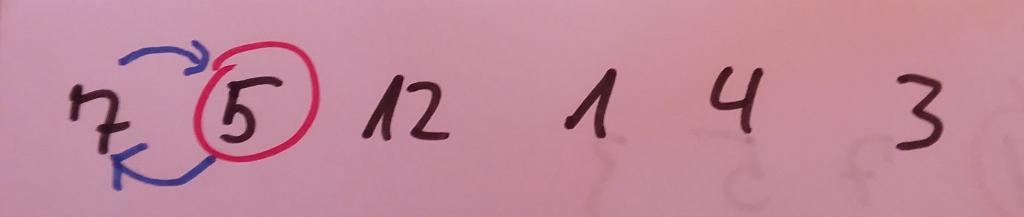
Damit ist die Aktion für das zweite Listenelement abgeschlossen. Für die weitere Sortierung ist es wichtig, zu berücksichtigen, dass sich damit die ersten beiden Positionen bereits in der richtigen Reihenfolge befinden. Das bedeutet, dass der erste Wert immer kleiner oder gleich groß ist wie der zweite Wert. Auf dieser Grundlage können wir uns dann dem nächsten Listenelement zuwenden. Die Aufgabe besteht hierbei wiederum darin, dieses aus der Liste zu entnehmen und an der passenden Stelle in den vorderen Bereich – der wie wir soeben festgestellt haben, bereits sortiert ist – einzuordnen. Dazu vergleichen wir den Wert mit dem Eintrag an der vorigen Stelle – in unserem Beispiel also die Zahlen 12 und 7. Dabei stellen wir fest, dass unser aktuelles Element größer ist als sein Vorgänger-Element. Da der komplette Bereich, der vor unserem Element steht, bereits sortiert ist, folgt daraus, dass sich auch an anderer Stelle kein Wert befindet, der größer als unser aktuelles Element ist. Daher belassen wir dieses an seiner Position. Das folgende Schaubild stellt dies dar.
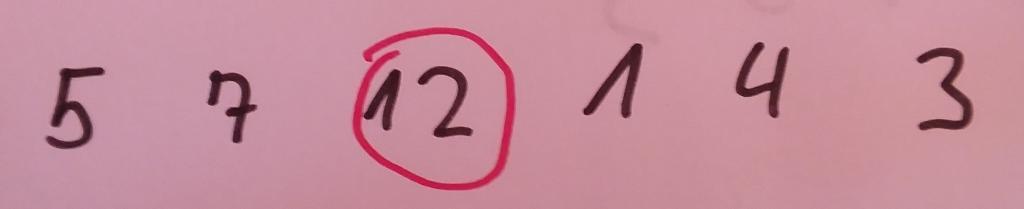
Nun können wir mit dem vierten Element fortfahren. Dieses weist den Wert 1 auf. Auch hierbei ist wieder festzuhalten, dass wir mit den bisherigen Maßnahmen sichergestellt haben, dass die Werte auf den Positionen 1 bis 3 bereits in sich sortiert sind. Daher entnehmen wir den Wert, der an der vierten Stelle der Liste steht und sortieren ihn an der passenden Stelle in die sortierte Teilliste ein. Dazu vergleichen wir ihn zunächst mit seinem Vorgängerelement – der Zahl 12. Diese ist größer als 1. Das bedeutet, dass wir das aktuelle Element vor ihr einordnen müssen. Daher verschieben wir die Zahl 12 eine Position nach hinten. Daraufhin vergleichen wir unser aktuelles Element mit dem Wert, der noch eine Position weiter vorne in der Liste steht – der Zahl 7. Auch diese ist größer, sodass wir sie eine Position nach hinten verschieben. Schließlich rücken wir noch eine Position vor und vergleichen den Eintrag mit der Zahl 5. Auch hier ist der Wert an der entsprechenden Position größer, sodass wir diesen nach hinten verschieben. Damit haben wir bereits den Anfang der Liste erreicht, sodass keine weiteren Vergleiche mehr möglich sind. Daher ordnen wir das aktuelle Element an der ersten Stelle ein – so wie dies in der folgenden Abbildung zu sehen ist.
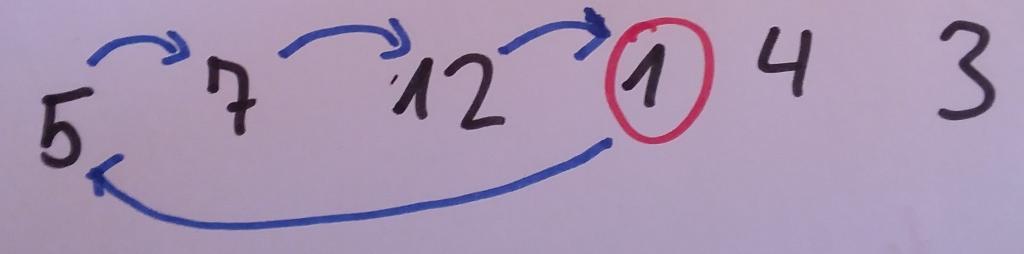
Auch dieser Schritt führt dazu, dass die Teilliste bis zur Position unseres aktuellen Elements in sich sortiert ist. Nun können wir mit dem fünften Element der Liste fortfahren. Hierbei gehen wir genau nach dem gleichen Muster vor: Wir vergleichen es mit dem Vorgängerelement. Ist es größer als dieses, belassen wir es an der entsprechenden Position. Ist es hingegen kleiner, verschieben wir den Inhalt, der sich dort befindet, eine Position weiter nach hinten und vergleichen unser Element mit dem Wert, der eine Position weiter vorne steht. Diesen Vorgang wiederholen wir so lange, bis wir entweder einen Wert gefunden haben, der kleiner als unser aktuelles Element ist oder bis wir den Anfang der Liste erreicht haben. Wenn wir dieses Verfahren auf das fünfte Element anwenden, führt das dazu, dass wir es an der zweiten Position der Liste einordnen. Die Elemente an den Positionen 2 bis 4 verschieben wir jeweils eine Position weiter nach hinten, so wie dies in der nächsten Abbildung zu sehen ist.
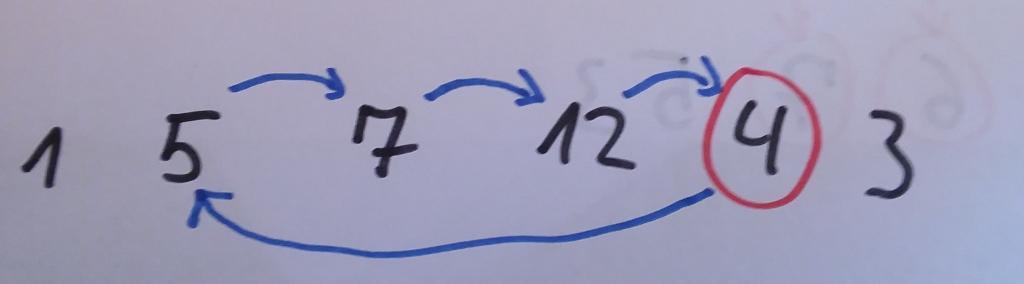
Nun müssen wir noch das letzte Element an der richtigen Stelle in die bereits sortierte Teilliste einordnen. Auch hierfür wenden wir wieder genau die gleiche Vorgehensweise an. Die folgende Abbildung illustriert dies:
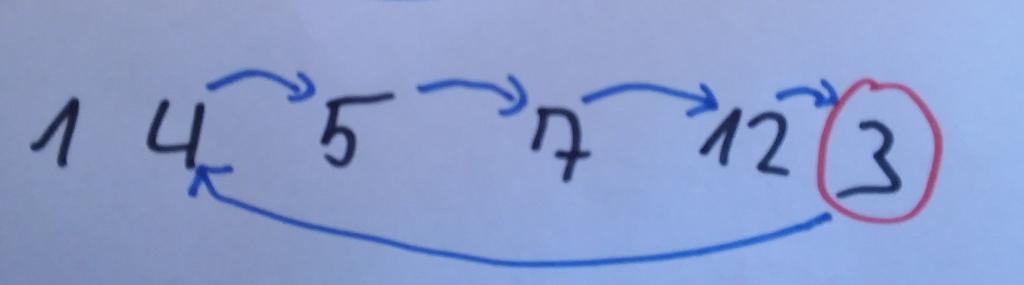
Damit haben wir das Ende der Liste erreicht. Da unser Verfahren sicherstellt, dass die Teilliste, die sich vor unserem aktuellen Element befindet, in sich sortiert ist, ist gewährleistet, dass nach der Bearbeitung des letzten Elements die komplette Liste sortiert ist. Daher haben wir unser Ziel erreicht und können den Vorgang beenden.
Ein Beispielprogramm für den Insertion-Sort-Algorithmus
Nun wollen wir noch ein Beispielprogramm für den Insertion-Sort-Algorithmus erstellen, damit Sie auch die praktische Anwendung kennenlernen und bei Bedarf den Code für ein eigenes Programm verwenden können. Hierbei verwenden wir genau wie in unseren bisherigen Beispielen die Programmiersprache C. Mit leichten Anpassungen lässt sich der Code jedoch auch in viele weitere Programmiersprachen übertragen.
Zunächst erstellen wir ein Array, das die Zahlen enthält, die wir sortieren möchten. Außerdem halten wir die Länge des Arrays fest. Danach erstellen wir drei Integer-Variablen i, j und k, die uns später als Zähler für verschiedene Schleifen dienen werden. Außerdem deklarieren wir die Variable aktuellesElement, in der wir bei jedem Durchgang den Wert des Elements abspeichern, das wir aus der Liste entfernen und neu einsortieren möchten.
Wie bereits beschrieben, müssen wir für den Insertion-Sort-Algorithmus die Schleife von der zweiten Position bis zu ihrem Ende durchgehen. Daher erstellen wir hierfür eine entsprechende for-Schleife:
for(i = 1; i < laenge; i++)
Darin weisen wir zuerst der Variable aktuellesElement den Wert unseres aktuellen Elements zu. Dieses erreichen wir über den Index i:
aktuellesElement = liste[i];
Daraufhin erstellen wir eine weitere Schleife. Diese soll die Liste von der Position unseres aktuellen Elements an in umgekehrter Reihenfolge durchgehen – entweder bis sie den Anfang der Liste erreicht hat oder bis sie ein Element gefunden hat, das kleiner als unser aktuelles Element ist. Daher erstellen wir zunächst den Zähler j für die innere Schleife und geben ihm den Wert der Position unseres aktuellen Elements – also i. Danach fügen wir die genannten Vorgaben als Bedingung für eine while-Schleife hinzu:
j = i; while(j > 0 && liste[j - 1] > aktuellesElement)
Wenn die Bedingung dieser Schleife zutrifft, bedeutet das, dass das Element an der Position j größer als unser aktuelles Element ist. Daher verschieben wir dieses einfach eine Position nach hinten. Daraufhin müssen wir nur noch den Wert des Zählers j um 1 erniedrigen und können die Schleife beenden:
liste[j] = liste[j - 1]; j--;
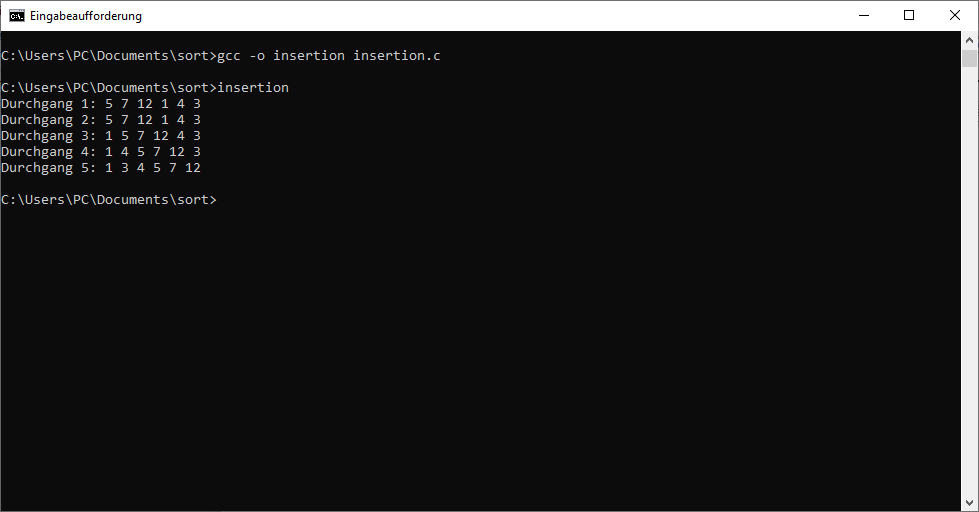
Wenn die Bedingung der while-Schleife nicht mehr zutrifft, ist sichergestellt, dass der Zähler j die Position angibt, an der wir das aktuelle Element einfügen müssen. Daher geben wir diesem Feld den Wert unseres aktuellen Elements. Damit ist unser Sortieralgorithmus beendet. Für eine anschaulichere Darstellung geben wir jedoch nach jedem Durchgang der äußeren for-Schleife noch den aktuellen Wert des Arrays aus. Das führt zu folgendem Programm:

Der Screenshot zeigt, dass das Programm die Liste auf diese Weise sortiert. Die Darstellung in den einzelnen Durchgängen entspricht dabei den oben vorgestellten Grafiken.
Insertion Sort: Nur in Ausnahmefällen ist die Verwendung sinnvoll
Zum Abschluss werfen wir noch einen kurzen Blick auf die Komplexität und auf die Anwendungsmöglichkeiten des Insertion-Sort-Algorithmus. Die Zahl der erforderlichen Rechenoperationen, die wir zum Sortieren der Liste benötigen, hängt stets von deren Länge ab. Um diese in die Berechnung einzubeziehen, verwenden wir dafür die Variable n. Im schlechtesten Fall – wenn die Liste genau in der umgekehrten Reihenfolge sortiert ist – müssen wir die äußere for-Schleife mit n – 1 Durchgängen durchlaufen. Die innere while-Schleife muss zunächst eine Operation durchführen, wobei die Anzahl bei jedem Durchgang um 1 ansteigt. Das führt zum Durchschnittswert n/2. Nun müssen wir diese beiden Zahlen miteinander multiplizieren. Das führt zu dem Ergebnis 1/2(n² – n). Dabei handelt es sich um einen quadratischen Term. Das hat zur Folge, dass die Zahl der erforderlichen Rechenoperationen bei längeren Listen ausgesprochen hoch ist. Daher ist die Verwendung in diesem Fall nicht zu empfehlen.
Im besten Fall – wenn die Liste bereits sortiert ist – müssen wir die innere Schleife überhaupt nicht ausführen. Daher bleibt nur noch die äußere Schleife, die wie bereits beschrieben die Anzahl n – 1 aufweist. Das zeigt, dass in diesem Fall nur sehr wenige Rechenoperationen notwendig sind.
Nun bleibt noch der Durchschnittsfall zu behandeln – also wenn die Werte in der Liste nach keinem vorgegebenen Muster geordnet sind. Diese Berechnung ist deutlich komplizierter, sodass sie hier nicht ausführlich vorgestellt werden kann. Das Ergebnis ist aber auch hierbei eine quadratische Gleichung, sodass die Effizienz sehr gering ist.
Das Verhalten ist daher sehr ähnlich wie beim Bubble-Sort-Algorithmus. Andere Sortieralgorithmen – beispielsweise Quicksort – weisen im Durchschnittsfall jedoch eine logarithmische Funktion auf. Das ist insbesondere bei langen Listen deutlich besser. Lediglich im besten Fall – wenn die Liste bereits zu Beginn sortiert ist, bietet der Insertion-Sort-Algorithmus Vorteile. Daher ist seine Verwendung nur dann zu empfehlen, wenn Sie davon ausgehen können, dass sich die Mehrheit der Listen, die Sie sortieren wollen, bereits weitestgehend in der richtigen Reihenfolge befindet.