Selectionsort: ein einfacher Sortieralgorithmus
Um eine Liste oder ein Array zu sortieren, gibt es zahlreiche Möglichkeiten. Die Vorgehensweise kann sich dabei erheblich unterscheiden. Daher stellen wir hier die häufigsten Sortier-Algorithmen nacheinander vor. Auf diese Weise erkennen Sie, welche Möglichkeiten es gibt und welche Vor- und Nachteile diese jeweils bieten. Dieser Artikel befasst sich mit dem Selectionsort-Algorithmus. Dieser zeichnet sich dadurch aus, dass er sehr einfach aufgebaut und daher leicht zu verstehen ist.
Das Sortierverfahren beim Selectionsort-Algorithmus
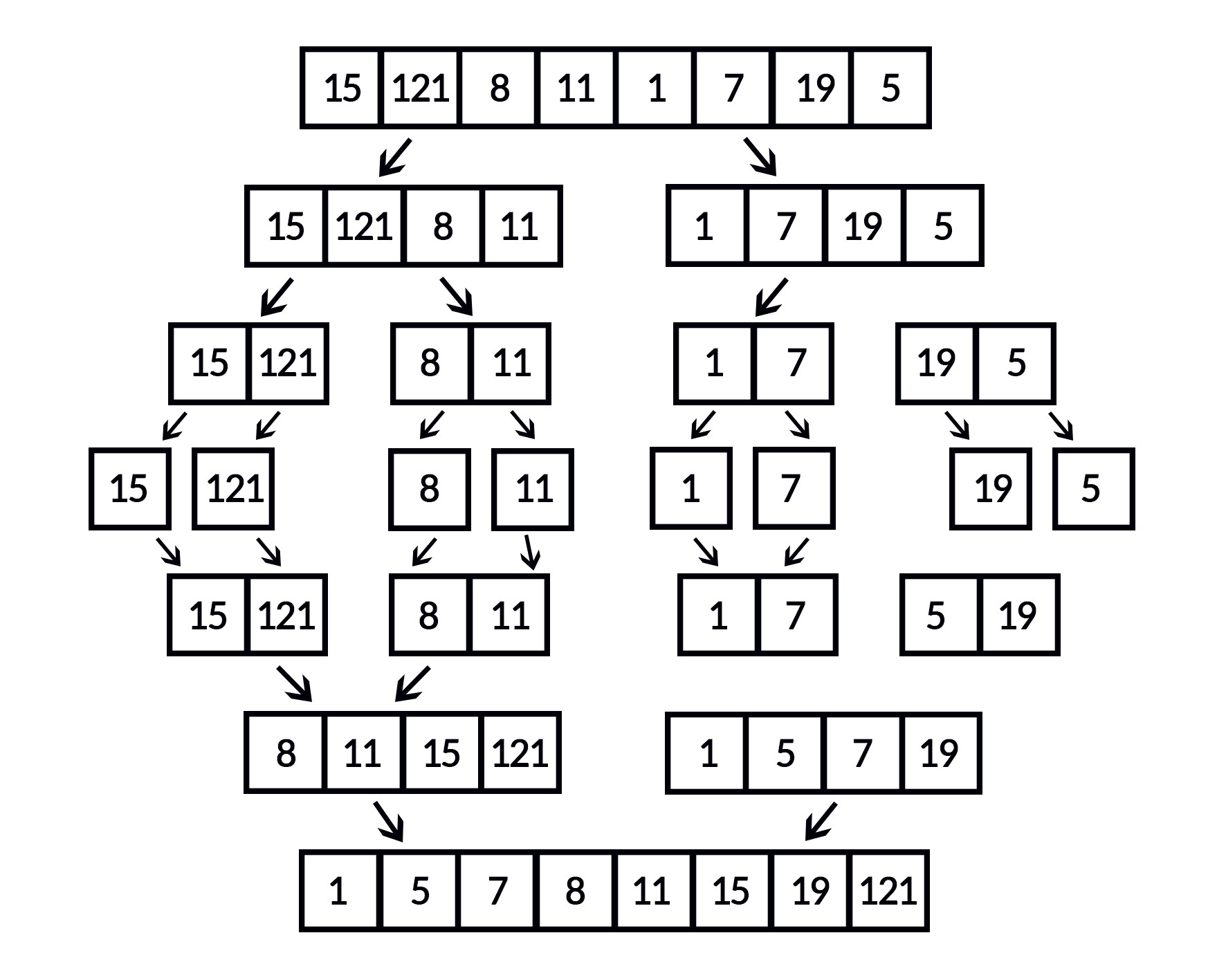
Die Vorgehensweise beim Selectionsort-Algorithmus ist ausgesprochen einfach. Dieser sucht zunächst das kleinste Element der gesamten Liste. Dieses tauscht er dann gegen das Element aus, das an erster Stelle der Liste steht. Die folgende Abbildung verdeutlicht diese Vorgehensweise.
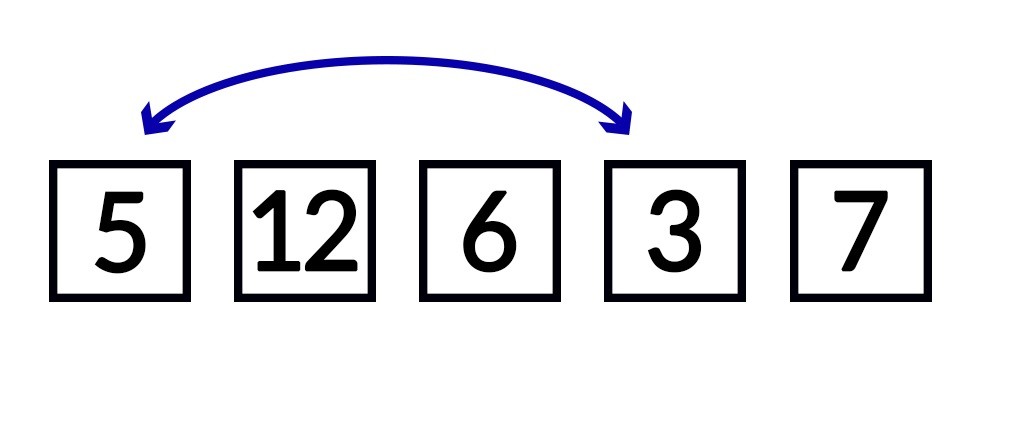
Im nächsten Schritt sucht der Algorithmus das zweitkleinste Element der Liste. Da bereits sichergestellt ist, dass das kleinste Element an der ersten Stelle steht, muss er hierfür die Liste nur ab dem zweiten Element durchgehen. In diesem Teilbereich sucht er dann das kleinste Element. Wenn er dieses gefunden hat, tauscht er dieses mit dem Element aus, das an zweiter Stelle in der Liste steht. Das wird an der folgenden Abbildung deutlich.
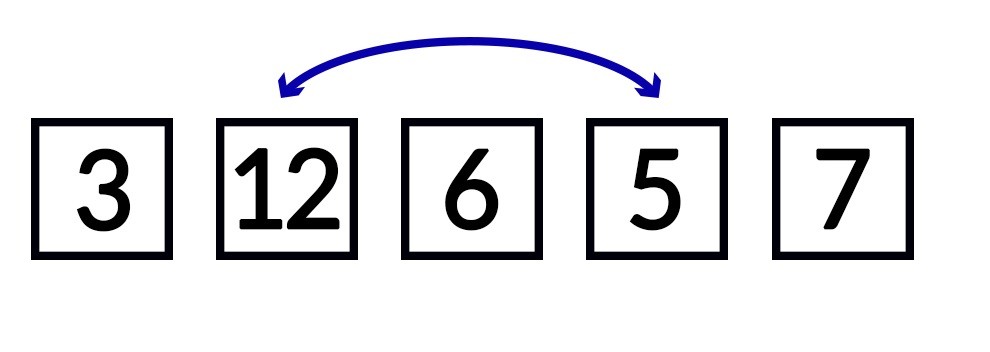
Dieses Verfahren wird auf die gleiche Weise weitergeführt. Im nächsten Schritt geht der Algorithmus die Liste ab der dritten Stelle durch und setzt das kleinste Element dieses Bereichs an die dritte Position. In unserem Beispiel steht die kleinste Zahl dieses Bereichs jedoch bereits an der richtigen Stelle. In diesem Fall ist keine weitere Aktion erforderlich.
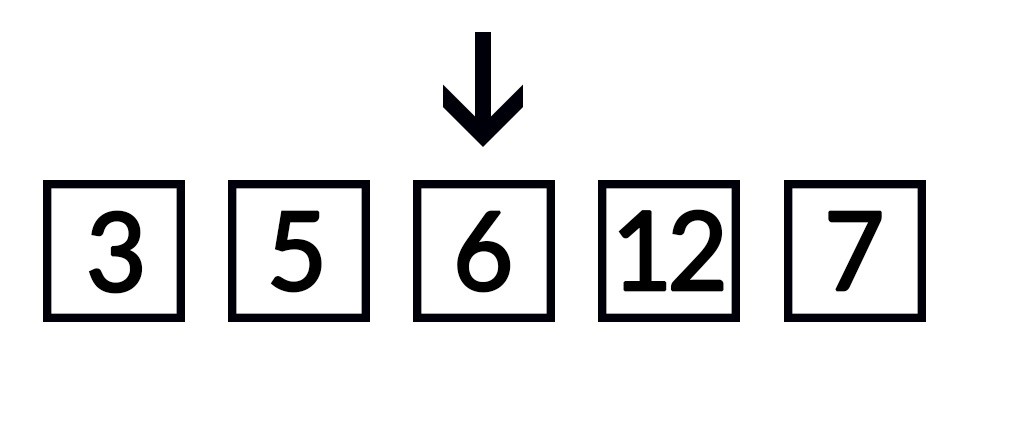
Nun folgt der vierte Schritt. Auch hier müssen wir des kleinste Element des Bereichs suchen, den wir noch nicht sortiert haben. In unserem Beispiel haben wir damit die vorletzte Position erreicht. Wenn wir das kleinste Element dieses Teilbereichs an die vierte Stelle gesetzt haben, ist sichergestellt, dass auch die letzte Position richtig besetzt ist. Daher können wir damit das Sortierverfahren beenden. Die Anzahl der Durchläufe ist immer um 1 niedriger als die Anzahl der Elemente der Liste.

Ein Beispielprogramm für Selectionsort
Nachdem das Verfahren des Selectionsort-Algorithmus vorgestellt wurde, erstellen wir noch ein kleines Beispielprogramm, um die Anwendung zu verdeutlichen. Wie bei allen unseren Beispielen für Sortieralgorithmen verwenden wir hierfür die Programmiersprache C. Doch ist es auch hierbei problemlos möglich, viele andere Programmiersprachen zu verwenden. Die grundsätzliche Vorgehensweise bleibt dabei stets die gleiche, sodass nur wenige Anpassungen notwendig sind.
Bestimmung der Variablen und Festlegung der Array-Größe
Der erste Schritt besteht darin, die erforderlichen Variablen zu deklarieren. Für dieses Programm benötigen wir zwei Schleifen – eine, um das Array Schritt für Schritt durchzugehen und eine weitere, um das kleinste Element im Bereich nach der aktuellen Position zu finden. Daher benötigen wir zwei Zähler, bei denen es sich selbstverständlich um natürliche Zahlen handelt. Außerdem ist eine Variable notwendig, um die Position des kleinsten Werts, den wir gefunden haben, festzuhalten. Schließlich benötigen wir später eine Hilfsvariable, um die Werte der beiden Positionen auszutauschen. Da unser Array natürliche Zahlen enthalten soll, müssen wir hierfür ebenfalls einen int-Wert deklarieren:
int i, j, position, tausch;
Anschließend erstellen wir ein beliebiges Array. Um hierbei mit flexiblen Größen arbeiten zu können, müssen wir anschließend bestimmen, wie viele Felder es enthält. Das erledigen wir in C mit der sizeof()-Funktion. Diese gibt jedoch die Länge des Arrays in Bytes zurück. Um die Zahl der Positionen zu bestimmen, ist es noch erforderlich, diesen Wert durch die Länge eines einzelnen Feldes zu teilen. Auch hierfür verwenden wir die sizeof()-Funktion:
int arr[] = {5, 12, 6, 3, 7};
int arr_groesse = sizeof(arr) / sizeof(arr[0]);Die äußere for-Schleife
Nun kann der eigentliche Sortier-Algorithmus beginnen. Dazu müssen wir eine for-Schleife erstellen, die das Array Schritt für Schritt durchgeht. Wie bereits bei der Erklärung der grundsätzlichen Vorgehensweise ausgeführt, können wir die Überprüfung jedoch nach der vorletzten Position abbrechen. Daher leiten wir die Schleife mit folgendem Befehl ein:
for(i = 0; i < arr_groesse - 1; i++)
Das kleinste Element finden
Die nächste Aufgabe besteht darin, die Position des kleinsten Elements innerhalb des noch nicht sortierten Bereichs zu finden. Dabei müssen wir nur den Bereich ab der aktuellen Position der äußeren Schleife durchgehen – da unser Sortieralgorithmus sicherstellt, dass die Elemente an den vorherigen Positionen bereits sortiert sind. Bevor wir hierfür eine for-Schleife erstellen, geben wir der Variable position jedoch den Wert des Zählers der äußeren Schleife – also i. Das bedeutet, dass wir zunächst einmal davon ausgehen, dass sich der kleinste Wert genau an dieser Position befindet. Diese Annahme wird dann in der inneren Schleife überprüft und falls notwendig berichtigt. Der hierfür erforderliche Befehl sieht so aus:
position = i;
Danach öffnen wir die for-Schleife. Dieses muss nur den Bereich überprüfen, der nach dem Feld steht, dessen Position durch die Variable i gekennzeichnet wird. Daher können wir den Zähler mit j = i + 1 initialisieren. Danach gehen wir das Array bis zu seinem Ende durch. Innerhalb der Schleife überprüfen wir lediglich, ob der entsprechende Wert kleiner als die Zahl in dem Feld ist, auf das die Variable position verweist. Trifft dies zu, weisen wir der Variable position den Wert des Zählers der inneren Schleife – also j – zu. Auf diese Weise halten wir fest, dass sich hier der kleinste Wert befindet, den wir bisher gefunden haben. Nachdem die Schleife beendet ist, ist deshalb sichergestellt, dass diese Variable die Position des kleinsten Elements innerhalb des kompletten Bereichs aufweist. Die vollständige Schleife sieht dann wie folgt aus:
Austausch der Elemente und Ausgabe des Arrays
Nun müssen wir noch das kleinste Element des Bereichs mit dem Wert an der Position i austauschen. Dazu verwenden wir die Hilfsvariable tausch, die den Wert eines der beiden Array-Felder aufnimmt, um den Austausch vorzunehmen. Selbstverständlich ist diese Aufgabe nur dann notwendig, wenn sich der kleinste Wert nicht bereits an der richtigen Stelle befindet. Daher setzen wir diesen Austausch in eine entsprechende if-Abfrage:
Danach können wir auch die äußere for-Schleife schließen. Damit ist unser Sortierverfahren abgeschlossen. Nun müssen wir nur noch das sortierte Array ausgeben:
Der komplette Programmcode
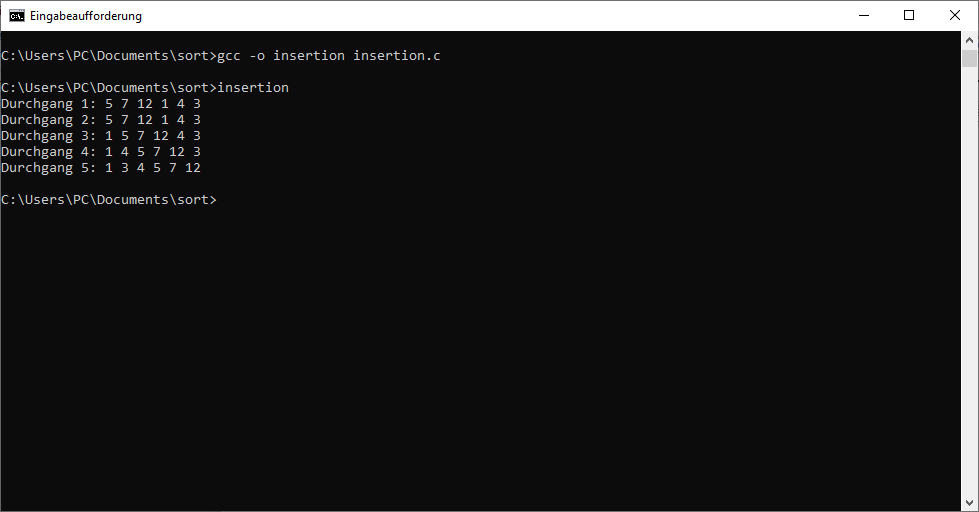
Wenn Sie die einzelnen Teile, die hier vorgestellt wurden, korrekt zusammengefügt haben, sollte das Programm bereits lauffähig sein. Zur Überprüfung geben wir hier jedoch nochmals den kompletten Code an. Danach folgt ein Screenshot, der den Ablauf des Programms aufzeigt.
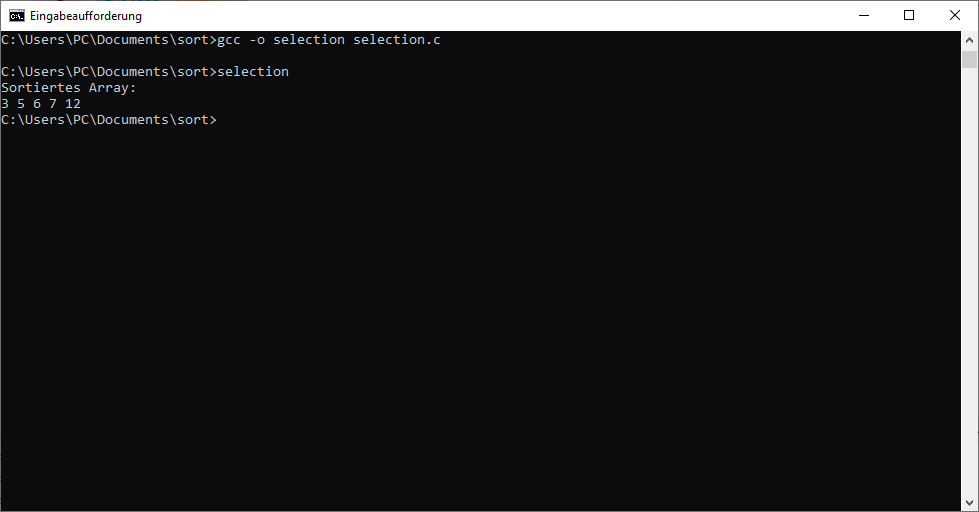
Selectionsort im Vergleich zu anderen Sortieralgorithmen
Zum Abschluss werfen wir noch einen Blick auf die Vor- und Nachteile des Selectionsort-Sortiervorgangs. Die Erklärung und die Programmgestaltung haben gezeigt, dass dieser Sortieralgorithmus sehr leicht verständlich und einfach zu implementieren ist. Der Code für dieses Programm ist deutlich kompakter als bei vielen anderen Sortieralgorithmen. Daher stellt Selectionsort insbesondere für Anfänger eine sehr beliebte Wahl dar. Wenn der Fokus auf einer schnellen Codeerstellung liegt, kommt er auch gelegentlich bei professionellen Programmen zum Einsatz.
Das ist jedoch nur sehr selten der Fall. Das liegt daran, dass dieses Sortierverfahren ausgesprochen ineffizient arbeitet. Der Grund dafür liegt darin, dass es hierbei notwendig ist, sehr viele Vergleiche durchzuführen. Wenn wir die Länge des Arrays mit der Variable n darstellen, sind beim ersten Durchlauf der äußeren Schleife n – 1, beim zweiten Durchlauf n – 2 und beim dritten Durchlauf n – 3 Vergleiche notwendig. Dieses Muster wird so lange fortgesetzt, bis das Ende des Arrays erreicht ist. Die Gesamtzahl der erforderlichen Vergleiche beträgt damit n²/2 – n/2. Das bedeutet, dass die Komplexitätsklasse dieses Algorithmus einer quadratischen Formel entspricht. Daher sind sehr viele Rechenschritte notwendig – insbesondere bei größeren Arrays. Es gibt deutlich effizientere Vorgehensweisen – beispielsweise das Quicksort- oder das Mergesort-Verfahren.

 C++ Programmieren für Einsteiger
C++ Programmieren für Einsteiger