Lineare Regression mit Python: ein wichtiger Algorithmus für Machine Learning.
Machine Learning gilt als eine der wichtigsten Zukunftstechnologien. Anhand dieser Technik kann ein Computersystem Daten selbstständig analysieren und auf dieser Basis Vorhersagen für die Zukunft treffen. Auf diese Weise lernt das Programm anhand der vorherigen Ereignisse, neue Ereignisse zu bewerten und kann daher Entscheidungen für den Umgang mit diesen treffen.
Um die Daten auszuwerten, kommen viele verschiedene Algorithmen zum Einsatz. Manchmal handelt es sich hierbei um neue Techniken, die speziell für das Machine Learning entwickelt wurden. In vielen Fällen kommen jedoch auch seit Langem bekannte statistische Verfahren zum Einsatz. Ein Beispiel hierfür ist die lineare Regression. Dabei handelt es sich um ein Verfahren, das bereits seit Jahrzehnten zum Einsatz kommt – beispielsweise um die Entwicklung von Börsen- oder Währungskursen vorherzusagen. Obwohl dieses Verfahren bereits seit Langem bekannt ist, ist es für das Machine Learning von großer Bedeutung. Dieser Artikel stellt vor, was die lineare Regression ist und wie sie sich berechnen lässt. Zum Abschluss folgt ein Implementierungsbeispiel für diesen Algorithmus anhand der Programmiersprache Python.
Wozu dient die Lineare Regression?
Die lineare Regression dient dazu, eine Datenmenge mit mehreren nummerischen Attributen auszuwerten. Um das an einem Beispiel zu verdeutlichen, könnten wir uns vorstellen, dass wir eine Klimabeobachtung durchführen. Dabei messen wir die Temperatur (in °C), die Wolkendichte (in %), die Uhrzeit und die Niederschlagsmenge pro Stunde (in mm/h). Ein entsprechender Datensatz könnte dann so aussehen: 18 °C, 45%, 17:00 Uhr, 14 mm/h. Nun führen wir regelmäßig solche Messungen durch und halten die Werte fest. Daraufhin wollen wir sie dazu nutzen, Vorhersagen für weitere Situationen zu treffen. Die lineare Regressionsanalyse dient immer nur dazu, einen Wert anhand aller weiteren Parameter vorherzusagen. In unserem Beispiel könnten wir beispielsweise die Niederschlagsmenge vorhersagen, wenn wir die Temperatur, die Bewölkungsdichte und die Uhrzeit kennen.
Bei der linearen Regression gehen wir stets davon aus, dass ein linearer Zusammenhang zwischen denn Werten besteht. Das bedeutet, dass die grundlegende Formel für den Zusammenhang zwischen den Werten so lautet:
f(x1, x2, x3, … xn) = a1 * x1 + a2 * x2 + a3 * x3 + … + an * xn + b
Das bedeutet, dass jeder Wert lediglich mit einem bestimmten Parameter multipliziert wird. Es ist nicht erlaubt, ihn zu quadrieren, die Wurzel zu ziehen oder andere Berechnungen damit durchzuführen. Die Funktion, die wir ermitteln, beschreibt demnach eine Gerade. Diese bezeichnen wir als Regressionsgerade.
Der Vorteil der linearen Regression besteht darin, dass diese besonders einfach zu berechnen ist. Allerdings führt die Einschränkung, dass es sich dabei um eine lineare Funktion handeln muss, dazu, dass sie sich den tatsächlichen Werten oftmals nicht allzu sehr annähert. Häufig wäre eine andere Kurvenform besser.
Die Aufgabe der linearen Regression besteht nun darin, alle Parameter – also die Werte a1, a2, a3, … an sowie den Wert für b – so zu wählen, dass die daraus entstehende Funktion die tatsächlichen Werte möglichst genau beschreibt. Dazu ist es notwendig, die Gerade so zu gestalten, dass die Abstände zwischen einem Messewert und dem zugehörigen Wert auf der Geraden so gering wie möglich sind. Bei der Regressionsanalyse arbeiten wir jedoch nicht mit den einfachen Abständen, sondern mit den quadrierten Abständen. Das führt dazu, dass Punkte, die einen besonders großen Abstand von der Regressionsgerade haben, stärker gewichtet werden.
Einfache lineare Regression und multiple lineare Regression
Bei der Berechnung der Regressionsgeraden unterscheiden wir zwischen der einfachen linearen Regression und der multiplen linearen Regression. Das soeben aufgeführte Beispiel stellt die multiple lineare Regression dar: Hierbei hängt ein Wert von mehreren anderen Werten ab. Die einfache lineare Regression stellt einen Sonderfall dar: Hierbei hängt der zu berechnende Wert nur von einem anderen Wert ab.
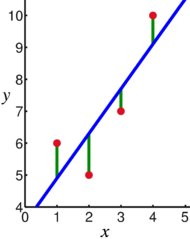
Die einfache lineare Regression ist nicht nur besonders einfach zu berechnen. Darüber hinaus kann man diese auch gut anhand eines Schaubilds darstellen. Die beiden zusammengehörigen Werte bilden einen Punkt in einem Koordinatensystem. Die zugehörige Funktion sieht dann so aus: f(x) = a * x + b.

Die obige Abbildung dient nicht nur dazu, die einfache lineare Regression bildlich darzustellen. Darüber hinaus wird daran deutlich, welche Abstände wir hier verwenden. Diese sind in grüner Farbe dargestellt. Dabei handelt es sich um senkrecht verlaufende Linien. Diese bestimmen nicht den minimalen Abstand zur Regressionsgeraden, sondern den Abstand zum Funktionswert an der entsprechenden Stelle.
Ein Algorithmus für die einfache lineare Regression
Um eine Gerade zu bestimmen, sind zwei Werte erforderlich – die Geradensteigung und der y-Achsen-Abschnitt. Diese entsprechen den Werten a und b in der oben vorgestellten Funktion. Bei grafischen Darstellungen wird die Steigung aber häufig auch mit dem Buchstaben m dargestellt. Die beiden Werte müssen wir nun separat berechnen.
Um die Geradensteigung zu berechnen, multiplizieren wir für jeden Punkt die Differenz zwischen dem x-Wert und dem Durchschnittswert aller x-Werte mit der Differenz zwischen dem y-Wert und dem Durchschnittswert aller y-Werte. Die Ergebnisse summieren wir dann für alle Punkte. Danach berechnen wir für jeden einzelnen Punkt die Differenz zwischen dessen x-Wert und dem Durchschnitt aller x-Werte. Diese Werte quadrieren wir zunächst und summieren sie dann für alle Punkte. Abschließend teilen wir die erste Summe durch die zweite Summe. Die mathematische Formel hierfür sieht dann so aus:
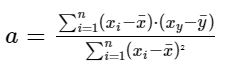
Der y-Achsen-Abschnitt lässt sich dann mithilfe der Steigung berechnen. Dazu müssen wir vom Durchschnittswert aller y-Werte den Durchschnitt der x-Werte multipliziert mit der Steigung abziehen:
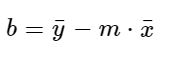
Die Implementierung mit Python
Anhand dieses Algorithmus können wir nun ein Python-Programm erstellen, das die Funktion für die Regressionsgerade anhand eines vorgegebenen Datensatzes ermittelt.
Dazu erstellen wir zunächst die entsprechenden Ausgangsdaten. Diese halten wir in einer zweidimensionalen Liste fest. Eine Liste mit fünf Datenpunkten könnte beispielsweise so aussehen:
daten = [[2, 6], [5, 7], [9, 3], [11, 19], [14, 18]]
Danach berechnen wir den Durchschnitt sowohl für die x-Werte als auch für die y-Werte:
summeX = 0
summeY = 0
for paar in daten:
summeX += paar[0]
summeY += paar[1]
durchschnittX = summeX / len(daten)
durchschnittY = summeY / len(daten)
Nach dieser Vorarbeit können wir nun nach der oben vorgestellten Formel die Steigung ermitteln:
summe1 = 0
for paar in daten:
summe1 += (paar[0] - durchschnittX) * (paar[1] - durchschnittY)
summe2 = 0
for paar in daten:
summe2 += pow((paar[0] - durchschnittX), 2)
steigung = summe1 / summe2
Nun ist es möglich, damit dem y-Achsen-Abschnitt zu berechnen:
yAchsenAbschnitt = durchschnittY - steigung * durchschnittX
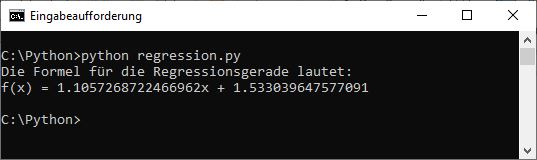
Damit haben wir alle erforderlichen Werte bereits berechnet. Wenn wir dann noch eine passende Ausgabe hinzufügen, sieht das gesamte Programm so aus:
daten = [[2, 6], [5, 7], [9, 3], [11, 19], [14, 18]]
summeX = 0
summeY = 0
for paar in daten:
summeX += paar[0]
summeY += paar[1]
durchschnittX = summeX / len(daten)
durchschnittY = summeY / len(daten)
summe1 = 0
for paar in daten:
summe1 += (paar[0] - durchschnittX) * (paar[1] - durchschnittY)
summe2 = 0
for paar in daten:
summe2 += pow((paar[0] - durchschnittX), 2)
steigung = summe1 / summe2
yAchsenAbschnitt = durchschnittY - steigung * durchschnittX
print("Die Formel für die Regressionsgerade lautet: ")
if yAchsenAbschnitt >= 0:
print(f"f(x) = {steigung}x + {yAchsenAbschnitt}")
else:
print(f"f(x) = {steigung}x - {yAchsenAbschnitt * -1}")
Bildquelle:
https://commons.wikimedia.org/wiki/File:Linear_least_squares_example2.png

 Hacking und IT-Security für Einsteiger
Hacking und IT-Security für Einsteiger 



