
Dynamische Programmierung
Wenn es darum geht, ein Computerprogramm zu schreiben, ist es zunächst notwendig, sich genau zu überlegen, worin das Problem besteht und auf welche Weise es möglich ist, dieses zu lösen. Dazu ist es notwendig, einen Algorithmus zu entwickeln, der das Problem Schritt für Schritt lösen kann und dabei stets zum richtigen Ergebnis kommt.
Algorithmen lassen sich in verschiedene Kategorien einteilen. Diese unterscheiden sich in ihrer Vorgehensweise und häufig auch in ihrer Effizienz. Dabei ist es wichtig, zu beachten, dass sich nicht jeder Algorithmus für jedes Problem eignet. Viele Algorithmen entsprechen dem Prinzip der dynamischen Programmierung. In diesem Artikel stellen wir vor, was dieser Begriff bedeutet.
Was bedeutet dynamische Programmierung?
Damit es möglich ist, das Prinzip der dynamischen Programmierung anzuwenden, ist es notwendig, dass das Problem, das Sie damit lösen wollen, zwei Grundvoraussetzungen erfüllt. Die erste davon lautet, dass sich das Problem in mehrere Teilprobleme zerlegen lässt und dass sich aus der Kombination ihrer Lösungen eine Lösung für das Gesamtproblem ergibt. Daraus geht hervor, dass die dynamische Programmierung einen rekursiven Ansatz verfolgt. Sie teilt das eigentliche Problem auf. Auf diese Teilprobleme wird dann wieder der gleiche Algorithmus angewendet. Dabei kann es dann zu einer neuen Aufteilung kommen. Dieser Prozess kann sich über mehrere Ebenen fortsetzen – so lange, bis keine weitere Aufteilung mehr notwendig ist und das entsprechende Teilproblem eine eindeutige Lösung hat.
Die zweite Bedingung besteht darin, dass sich diese Teilprobleme gegenseitig überlappen. Das bedeutet, dass es möglich ist, dass bei einer erneuten Zerlegung die Teilprobleme auf der nächsten Ebene identisch sein können. Entstehen keine identischen Teilprobleme, lässt sich ein Algorithmus, der die dynamische Programmierung umsetzt, zwar ebenfalls umsetzen. Allerdings bringt er in diesem Fall Nachteile gegenüber anderen Vorgehensweisen mit sich. Für Probleme ohne sich überlappende Teilprobleme ist es meistens sinnvoll, einen Algorithmus zu verwenden, der dem Prinzip „Divide and Conquer“ beziehungsweise „Teile und Herrsche“ entspricht.
Die Grundidee der dynamischen Programmierung besteht darin, die Ergebnisse aller Teilprobleme abzuspeichern, sobald diese vorliegen. Wenn daraufhin ein identisches Problem an anderer Stelle auftaucht, ist es meistens wesentlich effizienter, dessen Lösung aus dem Speicher abzurufen, als es erneut zu berechnen.
Erklärung anhand der Berechnung der Fibonacci-Folge
Diese etwas abstrakten Ausführungen wollen wir jetzt etwas anschaulicher gestalten. Dazu erklären wir die dynamische Programmierung am Beispiel der Fibonacci-Folge. Diese gibt für die Positionen 1 und 2 jeweils den Wert 1 vor. Der Wert für alle weiteren Positionen ergibt sich dann aus der Summe der beiden vorherigen Werte. Der Anfang der Folge sieht demnach so aus:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Wenn wir daraufhin den Wert an einer bestimmten Position berechnen wollen, müssen wir dazu den Wert an der vorherigen Position und den Wert an der Position zwei Stellen zuvor miteinander addieren. Die einzige Ausnahme stellen die Positionen 1 und 2 dar, bei denen jeweils der Wert 1 fest vorgegeben ist. Wenn wir den Wert an der Stelle n berechnen wollen und wir f() als Fibonacci-Funktion vorgeben, gilt demnach für alle n > 2:
f(n) = f(n – 1) + f(n – 2)
Für n <= 2 gilt hingegen f(n) = 1.
Auf diese Weise haben wir das ursprüngliche Problem in zwei Teilprobleme aufgeteilt, aus denen wir dann die Gesamtlösung ermitteln können. Damit erfüllt unser Problem die erste Bedingung für die Anwendung der dynamischen Programmierung.
Nun betrachten wir, wie dieser Algorithmus weiter verläuft. Wenn wir davon ausgehen, dass n so groß ist, dass keines der beiden Teilprobleme ein direktes Ergebnis liefert, müssen wir die oben angegebene Funktion erneut anwenden. Wir beschränken uns dabei zunächst auf f(n-1):
f(n-1) = f(n – 2) + f(n – 3)
Wenn wir dies in die oben angegebene Formel für f(n) einfügen, sieht diese wie folgt aus:
f(n) = f(n – 2) + f(n – 3) + f(n – 2)
Hier sehen wir, dass der Ausdruck f(n- 2) doppelt vorkommt. Das bedeutet, dass einige der Teilprobleme identisch sind. Es sind also sich überlappende Teilprobleme aufgetreten, sodass auch die zweite Bedingung erfüllt ist.
Bei der Verwendung eines einfachen rekursiven Algorithmus müssen wir die doppelten Teilprobleme auch doppelt berechnen. Es kommt hinzu, dass es noch zu vielen weiteren Dopplungen kommt. Gerade bei großen Zahlen führt das dazu, dass der Algorithmus sehr ineffizient arbeitet und viel Rechenzeit benötigt. Der Ansatz der dynamischen Programmierung besteht darin, alle Teilergebnisse, die wir berechnen, separat abzuspeichern. In unserem Beispiel würde das bedeutet, dass wir den Wert für f(n – 2) abspeichern, wenn wir ihn einmal berechnet haben. Bei der Ermittlung jedes weiteren Teilproblems überprüfen wir zuerst, ob wir das Ergebnis bereits berechnet haben. Ist dies der Fall, können wir es einfach übernehmen. Wenn wir dann f(n – 2) das zweite Mal aufrufen, ist keine erneute Berechnung notwendig. Das reduziert die erforderliche Rechenleistung deutlich.
Die Ursprünge der dynamischen Programmierung
Die dynamische Programmierung ist ein Begriff, der ursprünglich eher mit der Mathematik in Verbindung stand, als mit der Informatik. Der US-amerikanische Mathematiker Richard Bellman entwarf ihn bereits in den 1940er Jahren – als sich die Informatik gerade erst in ihrer Entstehung befand. Dieser entwickelte auch das sogenannte Optimalitätsprinzip von Bellman. Dieses besagt, dass sich die optimale Lösung für ein Problem aus den optimalen Lösungen seiner Teilprobleme ergibt. Dieses Optimalitätsprinzip stellt eine wichtige Grundlage für die dynamische Programmierung dar.
Das Rucksackproblem in der dynamischen Programmierung
Die dynamische Programmierung kommt besonders häufig zum Einsatz, um ein Optimierungsproblem zu lösen. Das bedeutet, dass wir aus mehreren verschiedenen Lösungen diejenige heraussuchen, die unseren Anforderungen am besten entspricht.
Ein Beispiel für ein solches Optimierungsproblem ist das sogenannte Rucksackproblem. Dieses besteht darin, dass uns ein Rucksack mit einer bestimmten Tragfähigkeit zur Verfügung steht. Darüber hinaus stehen verschiedene Gegenständen bereit. Diese weisen jeweils ein unterschiedliches Gewicht auf. Sie haben aber auch einen verschiedenen Wert. Das Verhältnis zwischen Gewicht und Wert weist dabei ebenfalls Unterschiede auf. Das Gesamtgewicht aller Gegenstände übersteigt die Tragfähigkeit des Rucksacks. Wir wollen jetzt den Rucksack so packen, dass wir den maximalen Wert darin transportieren, ohne die Tragfähigkeit zu übersteigen.

Dieses Problem können wir wieder mit einem rekursiven Algorithmus lösen. Dazu listen wir die verfügbaren Gegenstände der Reihe nach auf – jeweils mit ihrem jeweiligen Gewicht und ihrem Wert. Daraufhin gehen wir die Liste von oben nach unten durch. Dabei entscheiden wir jeweils, ob wir den entsprechenden Gegenstand einpacken oder nicht. Um diese Entscheidung zu treffen, müssen wir jedoch überprüfen, ob dies für ein optimales Ergebnis sinnvoll ist.
Um dies zu entscheiden, teilen wir das Problem wieder in zwei Teilprobleme auf. Die eine Möglichkeit besteht darin, dass wir den Gegenstand mitnehmen. In diesem Fall reduziert sich der freie Platz im Rucksack um dessen Gewicht und der Wert erhöht sich um dessen Wert. Die zweite Alternative besteht darin, dass wir ihn nicht mitnehmen. In diesem Fall bleiben der verfügbare Platz und der enthaltene Wert unverändert. Nun müssen wir für beide Alternativen wiederum jeweils die optimale Lösung finden. Dazu springen wir zum nächsten Gegenstand in der Liste und führen die gleichen Berechnungen aus. Das führt zu einem Entscheidungsbaum – so wie in der unten stehenden Abbildung dargestellt.
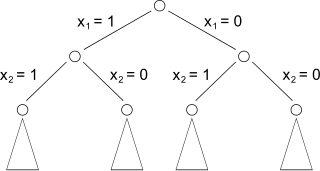
Diese Vorgehensweise führt uns stets zum richtigen Ergebnis. Allerdings ist sie sehr ineffizient – insbesondere bei einer sehr großen Menge an Gegenständen. Hierbei kommt es häufig vor, dass sich Berechnungen wiederholen. Deshalb ist es sinnvoll, die dynamische Programmierung für das Rucksackproblem zu verwenden. Dazu ist es jedoch zuerst notwendig, sich zu überlegen, wann wir überhaupt von einem gleichen Teilproblem sprechen können. Dieses tritt immer dann auf, wenn auf der gleichen Ebene die gleiche Kapazität vorhanden ist. In diesen Fällen ist die optimale Lösung des Teilproblems stets die gleiche – unabhängig davon, welche Gegenstände wir auf den oberen Ebenen eingepackt haben. Deshalb ist es sinnvoll für das Rucksackproblem die dynamische Programmierung anzuwenden und alle Teilergebnisse in einer separaten Liste zu notieren. Daraufhin prüfen wir vor jeder weiteren Berechnung, ob für das entsprechende Teilproblem bereits eine Lösung vorliegt. Das macht den Algorithmus deutlich effizienter.
Dynamische Programmierung und dynamische Programmiersprachen
Bei der Behandlung der dynamischen Programmierung kommt es immer wieder zu Verwechslungen mit dynamischen Programmiersprachen. Dabei ist es jedoch wichtig, zu beachten, dass es sich hierbei um zwei Begriffe handelt, die keine Verbindung zueinander aufweisen. Dynamische Programmiersprachen zeichnen sich dadurch aus, dass sie viele Aufgaben erst während der Laufzeit umsetzen, die andere Programmiersprachen bereits beim Kompilieren erledigen. Bekannte Beispiele für dynamische Programmiersprachen sind Python, JavaScript, PHP und Perl. Um Algorithmen mit dynamischer Programmierung zu implementieren, ist es jedoch nicht notwendig, eine dynamische Programmiersprache zu verwenden. Das ist auch mit jeder anderen höheren Programmiersprache möglich.
Fazit: Die dynamische Programmierung hilft bei Optimierungsproblemen
Die dynamische Programmierung erlaubt es, Lösungen für vielfältige Probleme mit hoher Effizienz zu berechnen. Zwar lässt sich diese Form der Problemlösung nicht immer umsetzen. Wenn die hierfür erforderlichen Bedingungen erfüllt sind, führt die dynamische Programmierung jedoch stets zu einer einfachen und effizienten Lösung.
Bildquellen:
https://commons.wikimedia.org/wiki/File:Knapsack.svg
https://commons.wikimedia.org/wiki/File:Arbre_binaire_exploration.svg





