Die O-Notation
Die O-Notation (auch Big-O-Notation oder Landau-Notation genannt) ist eigentlich ein Thema der Mathematik und wird verwendet, um asymptotisches Verhalten von Funktionen und Zahlenfolgen zu beschreiben. In der theoretischen Informatik wird die Notation genutzt, um Algorithmen zu analysieren und Aussagen über Komplexität, Laufzeit und benötigten Speicherplatz in Abhängigkeit der Eingabegröße zu treffen. Wir werden in diesem Artikel beleuchten, wie man die O-Notation verwendet, die Laufzeit einiger geläufigen Algorithmen näher betrachten und uns mit Best, Worst und Average Case-Laufzeiten beschäftigen.
Was ist die die O-Notation?
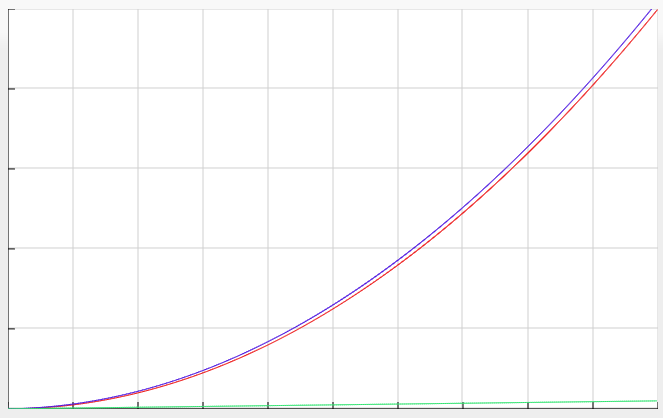
Wie bereits in der Einführung erwähnt, wird die O-Notation in der Mathematik dazu verwendet, asymptotisches Verhalten, also das Verhalten am Grenzwert, von Funktionen und Folgen festzustellen. Um zu verstehen, was genau das bedeutet, betrachten wir die Graphen der Funktionen f(n) = n², g(n) = n² + 3n und h(n)=2n.

Verfolgt man die Graphen, kann man sehen, dass die Funktionen f(n) und g(n) relativ gleich stark steigen, während die Funktion h(n) deutlich abflacht. Dieses Verhältnis kann durch die Landau-Notation ausgedrückt werden. Seien eine Funktion f und g gegeben, so schreibt man:
- f ∈ o(g), wenn f langsamer als g wächst
- f ∈ O(g), wenn f nicht wesentlich schneller (ähnlich schnell) wie g wächst
Für dieses Beispiel würde also gelten: f ∈ O(g), g ∈ O(f), h ∈ o(g), h ∈ o(f).
Weiterhin gilt: f, g ∈ O(n²), h ∈ O(n)
Grundsätzlich können bei der Landau-Notation Kostanten und Faktoren weggelassen werden, es gilt also beispielsweise 2n ∈ O(n) oder n + 3 ∈ O(n).
Wie wird die O-Notation in der Informatik angewandt?
Diese Notation kann man nun nutzen, um eine Aussage darüber zu treffen, wie sich Laufzeit oder Speicherplatz bei Algorithmen mit größer werdenden Eingaben verhalten.
Angenommen wir haben eine Methode, die als Eingabewert n Zeichenketten erhält, über diese Zeichenketten iteriert und sie einzeln ausgibt:
Die Ausgabe ist ein atomarer Schritt – also ein Schritt mit konstanter Laufzeit, der keine weiteren Teilschritte enthält – und wird n-mal ausgeführt. Die Laufzeit der Methode ist daher ungefähr doppelt so lang, wenn eine doppelt so große Menge an Zeichenketten eingegeben wird. Wir können sagen, die Funktion wächst in etwa so schnell wie die Funktion f(n)=n oder anders ausgedrückt: f ∈ O(n), wobei f die Funktion print_strings ist.
Würden wir über eine Eingabemenge n zweimal iterieren und einen atomaren Schritt ausführen, wie mit der folgenden Funktion, dann wäre die Laufzeit in O(n²), da wir für alle n Einträge n-mal den atomaren Schritt ausführen.
Welche Laufzeit ein Algorithmus hat ist natürlich nicht immer so offensichtlich wie in unseren Beispielen. Trotzdem kann man jeden Algorithmus in eine Klasse einordnen. Die häufigsten sind die folgenden:
| Notation | Erklärung | Beispiele |
| f ∈ O(1) | Die Funktion hat eine konstante Laufzeit | ⦁ Einfache Prüfung, ob eine Binärzahl gerade ist ⦁ Zugriff auf einen bestimmten Index einer Liste |
| f ∈ O(log n) | Logarithmische Laufzeit, d.h. wenn sich die Eingabegröße n verdoppelt, wächst die Laufzeit der Funktion um einen konstanten Betrag | ⦁ Binäre Suche auf einem sortierten Feld, d.h. der Suchbereich wird halbiert bis das gesuchte Element gefunden wurde |
| f ∈ O(n) | Lineares Wachstum, d.h. wenn n sich verdoppelt, verdoppelt sich auch die Laufzeit | ⦁ Lineare Suche, d.h. jedes Element wird nacheinander betrachtet bis das gesuchte Element gefunden wurde |
| f ∈ O(n log n) | Super-lineares Wachstum | ⦁ Sortieralgorithmen auf Basis von Vergleichen wie Heapsort oder Mergesort |
| f ∈ O(n²) | Quadratische Laufzeit, d.h. wenn n sich verdoppelt, vervierfacht sich die Laufzeit | ⦁ Einfache Sortieralgorithmen wie Bubblesort oder Selectionsort |
| f ∈ O(2^n) | Exponentielles Wachstum, d.h. wenn n sich um 1 erhöht, verdoppelt sich die Laufzeit | ⦁ SAT, das Entscheidungsproblem darüber, ob eine aussagenlogische Formel erfüllbar ist (von englisch satisfiability) |
| f ∈ O(n!) | Faktorielles Wachstum, d.h. wenn n um 1 wächst, wächst die Laufzeit um etwa n+1 | ⦁ Problem des Handlungsreisenden |
Generell gilt, dass exponentielle oder sogar faktorielle Laufzeiten für große Eingaben zu extrem langen Rechenzeiten führen. Daher werden für bekannte Probleme der Mathematik und Informatik stets effektivere Algorithmen oder Beweise für die bestmögliche Laufzeit gesucht. So ist es unter anderem bewiesen, dass ein Suchalgorithmus ohne Vorinformation über die Eingabe niemals schneller als O(n log n) sein kann.
Best Case, Worst Case and Average Case
Für viele Algorithmen unterscheidet sich die Laufzeit je nachdem, ob die Eingabe dem besten, schlechtesten oder einem durchschnittlichen Fall entspricht. Betrachten wir dazu einen Suchalgorithmus wie Bubblesort:
Bei Bubblesort soll eine Liste mit vergleichbaren Elementen sortiert werden. Dazu wird die Liste in ihrer Reihenfolge iteriert und alle Elemente, die nicht in der richtigen Reihenfolge zu ihrem Nachbarn sind, werden getauscht. Dieses Vorgehen wird so lange über die ganze Liste ausgeführt, bis kein Tausch mehr durchgeführt wurde, also alle Elemente in richtiger Reihenfolge sind. Falls Sie Bubblesort noch nicht kennen, finden Sie ein kleines Beispiel am Ende des Artikels. Außerdem haben wir eine Blogartikelserie zu den verschiedenen Sortieralgorithmen inklusive Bubblesort.
Im besten Fall für Bubblesort sind alle Elemente bereits sortiert. Dann muss die Liste nur einmal iteriert werden, sodass Bubblesort eine Laufzeit von O(n) mit O(n) Vergleichen und O(1) Swaps hat.
Der schlimmste Fall hingegen ist eine invertierte Liste. Dann muss die Liste n-mal durchlaufen und jeweils alle Elemente getauscht werden, sodass sowohl O(n²) Vergleiche als auch Swaps durchgeführt werden müssen. Für den Best und Worst Case von Bubblesort finden Sie ebenfalls ein Beispiel am Artikelende.
In der Praxis ist der beste Fall für die Analyse eines Algorithmus meist nicht relevant: Interessanter sind der durchschnittliche und schlechteste Fall. Es gibt Algorithmen, die einen schlechteren Worst Case aber einen besseren Average Case als ein vergleichbarer Lösungsansatz haben. Insofern der Worst Case als Eingabe eher ein Ausnahmefall ist, wäre der Algorithmus mit dem besseren Average Case vorzuziehen. Ein Beispiel hierfür sind der Simplex Algorithmus und die Ellipsoidmethode der linearen Optimierung.
Andererseits gibt es Algorithmen, bei denen es relevant ist, das obere Limit der Laufzeit mit Sicherheit zu kennen und nicht versehentlich zu überschreiten. Zudem ist es für manche Anwendungsfälle schwierig, genau festzulegen, was eine „durchschnittliche“ Eingabe ist. In diesen Fällen ist die Betrachtung des Worst Case ausschlaggebend.
Insbesondere wenn sich schlechteste und durchschnittliche Laufzeit stark unterscheiden, kann die Komplexität über eine theoretisch unendliche Anzahl an Durchläufen amortisiert werden, sodass ein sicheres aber gleichzeitig realistisches oberes Limit ermittelt wird.
Zusammenfassung
Die O-Notation wird in der Informatik dafür verwendet, die Komplexität, die Laufzeit oder den Speicherbedarf eines Algorithmus im Hinblick auf die Eingabegröße zu bewerten. Man unterscheidet verschiedene Komplexitätsklassen, unter anderem mit konstantem, linearem, exponentiellem oder faktoriellem Wachstum. Für viele bekannte Gruppen von Algorithmen ist bereits bewiesen, welche Komplexität sie mindestens besitzen – beispielsweise O(n log n) für Sortieralgorithmen.
In der Praxis werden bei der Auswahl eines Algorithmus oder Analyse eines Problems meist der durchschnittliche oder schlechteste Fall (Average oder Worst Case) der Laufzeit betrachtet. Der schlechteste Fall beschreibt die Laufzeit des Algorithmus unter den ungünstigsten Bedingungen und kommt in der Praxis nicht immer vor. Der Average Case ist zwar meist realistischer, gibt aber kein gesichertes oberes Limit und kann für manche Probleme nur schwer definiert werden.
Beispiel Bubblesort
Die Eingabe ist 1 4 3 2.
⦁ Schritt
1 4 3 2 – korrekt
1 4 3 3 – nicht korrekt → 1 3 4 2
1 3 4 2 – nicht korrekt → 1 3 2 4
⦁ Schritt
1 3 2 4 – korrekt
1 3 2 4 – nicht korrekt → 1 2 3 4
1 2 3 4 – korrekt
⦁ Schritt
1 2 3 4 – korrekt
1 2 3 4 – korrekt
1 2 3 4 – korrekt
Damit ist die Sortierung beendet
Beispiel Bubblesort – Best Case
Die Eingabe ist 1 2 3 4.
⦁ Schritt
1 2 3 4 – korrekt
1 2 3 4 – korrekt
1 2 3 4 – korrekt
Damit ist die Sortierung beendet.
Beispiel Bubblesort – Worst Case
Die Eingabe ist 4 3 2 1.
⦁ Schritt
4 3 2 1 – nicht korrekt → 3 4 2 1
3 4 2 1 – nicht korrekt → 3 2 4 1
3 2 4 1 – nicht korrekt → 3 2 1 4
⦁ Schritt
3 2 1 4 – nicht korrekt → 2 3 1 4
2 3 1 4 – nicht korrekt → 2 1 3 4
2 1 3 4 – korrekt
⦁ Schritt
2 1 3 4 – nicht korrekt → 1 2 3 4
1 2 3 4 – korrekt
1 2 3 4 – korrekt
⦁ Schritt
1 2 3 4 – korrekt
1 2 3 4 – korrekt
1 2 3 4 – korrekt





